题目内容
15.设向量$\overrightarrow a=({-1,2}),\overrightarrow b=({m,1})$,若向量$\overrightarrow a+2\overrightarrow b$与$2\overrightarrow a-\overrightarrow b$平行,则m=-$\frac{1}{2}$.分析 根据平面向量的坐标运算与共线定理,列出方程求出m的值.
解答 解:向量$\overrightarrow a=({-1,2}),\overrightarrow b=({m,1})$,
∴$\overrightarrow a+2\overrightarrow b$=(2m-1,4),
$2\overrightarrow a-\overrightarrow b$=(-2-m,3);
若向量$\overrightarrow a+2\overrightarrow b$与$2\overrightarrow a-\overrightarrow b$平行,
则3(2m-1)-4(-2-m)=0,
解得m=-$\frac{1}{2}$.
故答案为:-$\frac{1}{2}$.
点评 本题考查了平面向量的坐标运算与共线定理的应用问题,是基础题目.

练习册系列答案
相关题目
7.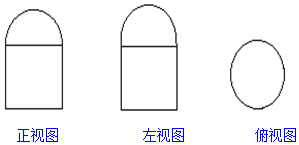 如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
 如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )| A. | 5π | B. | 6π | C. | 7π | D. | 8π |
 如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD.
如图,在四棱锥P-ABCD中,AD∥BC,AB⊥AD,AB⊥PA,BC=2AB=2AD=4BE,平面PAB⊥平面ABCD.