题目内容
1.若0<x<1,则$\frac{1}{x}+\frac{2x}{1-x}$的最小值为( )| A. | $2\sqrt{2}$ | B. | 1+$2\sqrt{2}$ | C. | 2+$2\sqrt{2}$ | D. | 3+$2\sqrt{2}$ |
分析 根据基本不等式的性质求出代数式的最小值即可.
解答 解:∵0<x<1,∴$\frac{1}{x}$-1>0,
∴$\frac{1}{x}+\frac{2x}{1-x}$=$\frac{1}{x}$-1+$\frac{2}{\frac{1}{x}-1}$+1≥2$\sqrt{(\frac{1}{x}-1)•\frac{2}{(\frac{1}{x}-1)}}$+1=1+2$\sqrt{2}$,
当且仅当$\frac{1}{x}$-1=$\frac{2}{\frac{1}{x}-1}$即x=$\sqrt{2}$-1时“=”成立,
故选:B.
点评 本题考查了基本不等式的性质,注意应用性质满足的条件,本题是一道基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
11.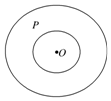 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
 如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )
如图,“天宫一号”运行的轨迹是如图的两个类同心圆,小圆的半径为2km,大圆的半径为4km,卫星P在圆环内无规则地自由运动,运行过程中,则点P与点O的距离小于3km的概率为( )| A. | $\frac{1}{12}$ | B. | $\frac{5}{12}$ | C. | $\frac{1}{3}$ | D. | $\frac{1}{5}$ |
7.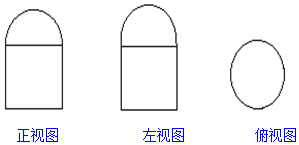 如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
 如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )
如图所示,是一个组合体的三视图,图中四边形是边长为2的正方形,圆的直径为2,那么这个组合体的表面积是( )| A. | 5π | B. | 6π | C. | 7π | D. | 8π |
8.若某几何体的三视图(单位:cm)如图所示,则该几何体的体积等于( )
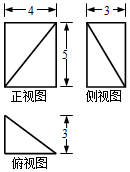

| A. | 10cm3 | B. | 20cm3 | C. | 30cm3 | D. | 40cm3 |
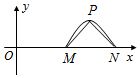 函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象关于y轴对称,该函数的部分图象如图所示,△PMN是以MN为斜边的等腰直角三角形,且$|MN|•|MP|=2\sqrt{2}$,则f(1)的值为0.
函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<π)的图象关于y轴对称,该函数的部分图象如图所示,△PMN是以MN为斜边的等腰直角三角形,且$|MN|•|MP|=2\sqrt{2}$,则f(1)的值为0.