题目内容
9.设a=log23,b=log3$\frac{1}{2}$,$c={(\frac{1}{2})^3}$,则a、b、c的大小关系是( )| A. | a<b<c | B. | c<b<a | C. | b<c<a | D. | a<c<b |
分析 利用指数函数与对数函数的单调性即可得出.
解答 解:∵a=log23>1,b=log3$\frac{1}{2}$<0,$c={(\frac{1}{2})^3}$∈(0,1),
∴b<c<a.
故选:C.
点评 本题考查了指数函数与对数函数的单调性,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
19.已知实数x,y满足$\left\{\begin{array}{l}x-2y+1≥0\\ x≤2\\ x+y-1≥0\end{array}\right.,z=|{x+2y-4}|$,则z的最大值与最小值之差为( )
| A. | 5 | B. | 1 | C. | 4 | D. | $\frac{7}{3}$ |
19.已知数列{an}的首项a1=1,对?n∈N*,都有an+1-an≤3n,an+2-an≥4•3n成立,则a2017=( )
| A. | 32017-1 | B. | $\frac{{3}^{2017}-1}{2}$ | C. | 32017+1 | D. | $\frac{{3}^{2017}+1}{2}$ |
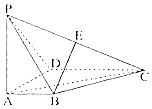 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.