题目内容
14.若倾斜角为45°的直线m被平行线l1:x+y-1=0与l2:x+y-3=0所截得的线段为AB,则AB的长为$\sqrt{2}$.分析 求出平行线l1:x+y-1=0与l2:x+y-3=0的距离d.倾斜角为45°的直线m与此两条平行线垂直,可得倾斜角为45°的直线m被平行线l1:x+y-1=0与l2:x+y-3=0所截得的线段为AB=d.
解答 解:平行线l1:x+y-1=0与l2:x+y-3=0的距离d=$\frac{|-3+1|}{\sqrt{2}}$=$\sqrt{2}$.
∴倾斜角为45°的直线m与此两条平行线垂直,因此被平行线l1:x+y-1=0与l2:x+y-3=0所截得的线段为AB=$\sqrt{2}$.
故答案为:$\sqrt{2}$.
点评 本题考查了点到直线的距离公式、直角三角形边角关系,考查了推理能力与计算能力,属于基础题.

练习册系列答案
相关题目
5.阅读如下程序框图,如果输出i=1008,那么空白的判断框中应填入的条件是( )

| A. | S<2014 | B. | S<2015 | C. | S<2016 | D. | S<2017 |
9.设a=log23,b=log3$\frac{1}{2}$,$c={(\frac{1}{2})^3}$,则a、b、c的大小关系是( )
| A. | a<b<c | B. | c<b<a | C. | b<c<a | D. | a<c<b |
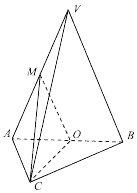 如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,VA=VB=4,AC=BC=2且AC⊥BC,O,M分别为AB,VA的中点.
如图,在三棱锥V-ABC中,平面VAB⊥平面ABC,VA=VB=4,AC=BC=2且AC⊥BC,O,M分别为AB,VA的中点.


