题目内容
18.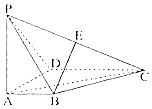 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥AB,AB∥DC,AD=DC=AP=1,$AB=\frac{1}{2}$,点E为棱PC的中点.(1)求直线BE与AD所成角的大小;
(2)证明:BE⊥DC.
分析 (1)取PD中点M,连结EM,AM.推导出四边形ABEM为平行四边形,从而BE∥AM,进而∠MAD为异面直线BE与AD所成角(或补角),由此能求出异面直线BE与AD所成角.
(2)推导出PA⊥CD,CD⊥DA,从而CD⊥平面PAD,进而CD⊥AM,再由BE∥AM,能证明BE⊥CD.
解答 解:(1)如图,取PD中点M,连结EM,AM.
由于E,M分别为PC、PD的中点,故$EM\underline{\underline{∥}}\frac{1}{2}DC$;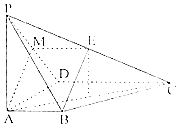
又$AB\underline{\underline{∥}}\frac{1}{2}DC,EM\underline{\underline{∥}}AB$,
∴四边形ABEM为平行四边形,∴BE∥AM.
∴∠MAD为异面直线BE与AD所成角(或补角),
在Rt△PAD中,∵AD=DC=AP=1,∴∠MAD=45°,
∴异面直线BE与AD所成角为45°.…(6分)
证明:(2)∵PA⊥底面ABCD,故PA⊥CD,
而CD⊥DA,CD∩DA=D,∴CD⊥平面PAD,
∵AM?平面PAD,∴CD⊥AM,
又由(1)得BE∥AM,
∴BE⊥CD.…(12分)
点评 本题考查两条异面直线所成角的大小的求法,考查线线垂直的证明,是中档题,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
8.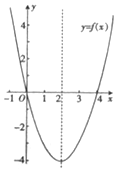 已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )
已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )
 已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )
已知函数f(x)的图象如图所示,则函数g(x)=log${\;}_{\frac{1}{2}}$f(x)的单调递增区间为( )| A. | (-∞,0) | B. | (4,+∞) | C. | (-∞,2) | D. | (2,+∞) |
9.设a=log23,b=log3$\frac{1}{2}$,$c={(\frac{1}{2})^3}$,则a、b、c的大小关系是( )
| A. | a<b<c | B. | c<b<a | C. | b<c<a | D. | a<c<b |




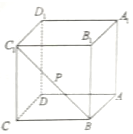 如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题:
如图,点P是正方体ABCD-A1B1C1D1的面对角线BC1(线段BC1)上运动,给出下列五个命题: