题目内容
4.已知x满足$\sqrt{3}≤{3^x}≤9$.(1)求 x 的取值范围;
(2)求函数$y=({log_2}^x-1)({log_2}^x+3)$的值域.
分析 (1)直接由指数函数的单调性,求得x的取值范围;
(2)由(1)中求得的x的范围,得到log2x的范围,令t=log2x换元,再由二次函数的图象和性质求得函数$y=({log_2}^x-1)({log_2}^x+3)$的值域.
解答 解:(1)∵$\sqrt{3}≤{3^x}≤9$,
∴${3^{\frac{1}{2}}}≤{3^x}≤{3^2}$,
由于指数函数y=3x在R上单调递增,
∴$\frac{1}{2}≤x≤2$;
(2)由(1)得$\frac{1}{2}≤x≤2$,
∴-1≤log2x≤1,
令t=log2x,则y=(t-1)(t+3)=t2+2t-3,其中t∈[-1,1],
∵函数y=t2+2t-3开口向上且对称轴为t=-1,
∴函数y=t2+2t-3在t∈[-1,1]上单调递增,
∴y的最大值为f(1)=0,最小值为f(-1)=-4.
∴函数y=(log2x-1)(log2x+3)的值域为[-4,0].
点评 本题考查指数不等式的解法,训练了函数值域的求法,属中档题.

练习册系列答案
相关题目
14.对于常数m、n,“关于x的方程x2-mx+n=0有两个正根”是“方程mx2+ny2=1的曲线是椭圆”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分不必要条件 |
15.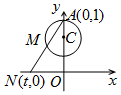 如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
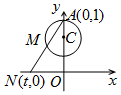 如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )
如图,周长为1的圆的圆心C在y轴上,一动点M从圆上的点A(0,1)开始按逆时针方向绕圆运动一周,记走过的弧长为x,直线AM与x轴交于点N(t,0),则函数t=f(x)的图象大致为( )| A. | 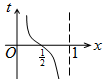 | B. | 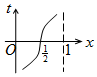 | C. | 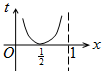 | D. | 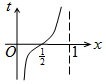 |
9.设a=log23,b=log3$\frac{1}{2}$,$c={(\frac{1}{2})^3}$,则a、b、c的大小关系是( )
| A. | a<b<c | B. | c<b<a | C. | b<c<a | D. | a<c<b |