题目内容
从某批次的灯泡中随机地抽取200个样品,对其使用寿命进行实验检测,将结果列成频率分布表如下.根据寿命将灯泡分成一等品、合格品和次品三个等级,其中寿命大于或等于500天的灯泡是一等品,寿命小于300天的灯泡是次品,其余的灯泡是合格品.
(Ⅰ)根据频率分布表中的数据,写出a,b的值;
(Ⅱ)从灯泡样品中随机地取n(n∈N*)个,如果这n个灯泡的等级分布情况恰好与从这200个样品中按三个等级分层抽样所得的结果相同,求n的最小值;
(Ⅲ)从这200个样品中按三个等级分层抽样抽取8个灯泡,再从这8个中抽取2个进行检测,求这2个灯泡中恰好一个是合格品一个是次品的概率.
| 寿命(天) | 频数 | 频率 |
| [100,200) | 20 | a |
| [200,300) | 30 | 0.15 |
| [300,400) | b | 0.35 |
| [400,500) | 30 | 0.15 |
| [500,600) | 50 | 0.25 |
| 合计 | 200 | 1 |
(Ⅱ)从灯泡样品中随机地取n(n∈N*)个,如果这n个灯泡的等级分布情况恰好与从这200个样品中按三个等级分层抽样所得的结果相同,求n的最小值;
(Ⅲ)从这200个样品中按三个等级分层抽样抽取8个灯泡,再从这8个中抽取2个进行检测,求这2个灯泡中恰好一个是合格品一个是次品的概率.
考点:列举法计算基本事件数及事件发生的概率,频率分布表
专题:概率与统计
分析:(Ⅰ)由频率分布表,得频率之和为1,频数之和为200,由此能求出a和b.
(Ⅱ)由表可知:灯泡样品中优等品有50个,正品有100个,次品有50个,优等品、正品和次品的比例为50:100:50=1:2:1.由此按分层抽样法,能求出n的最小值.
(Ⅲ)计算分层抽样的抽取比例,可得每组抽取个数;利用列举法写出从8个中随机抽取2个的所有基本事件,分别计算总个数与2个灯泡中恰好一个是合格品一个是次品的个数,根据古典概型概率公式计算.
(Ⅱ)由表可知:灯泡样品中优等品有50个,正品有100个,次品有50个,优等品、正品和次品的比例为50:100:50=1:2:1.由此按分层抽样法,能求出n的最小值.
(Ⅲ)计算分层抽样的抽取比例,可得每组抽取个数;利用列举法写出从8个中随机抽取2个的所有基本事件,分别计算总个数与2个灯泡中恰好一个是合格品一个是次品的个数,根据古典概型概率公式计算.
解答:
解:(Ⅰ)由频率分布表,得:
a=1-0.15-0.35-0.15-0.25=0.1.
b=200-20-30-30-50=70.
(Ⅱ)由表可知:灯泡样品中优等品有50个,正品有100个,次品有50个,
∴优等品、正品和次品的比例为50:100:50=1:2:1.
∴按分层抽样法,购买灯泡数n=k+2k+k=4k(k∈N*),
∴n的最小值为4.
(Ⅲ)利用分层抽样在200个样品中抽取8个灯泡,每个等级抽取的个数分别为:
一等品的个数为8×
=2,合格品的个数为8×
=4,次品的个数为8×
=2,
所以从一等品、合格品、次品分别抽取2个,4个,2个.
设一等品的2个为A、B,合格品的4个为C1、C2、C3、C4,次品的2个为D、E,
则从8个灯泡中随机抽取2个有:(A,B),(A,C1),(A,C2),(A,C3),
(A,C4),(A,D),(A,E),(B,C1),(B,C2),(B,C3),(B,C4),
(B,D),(B,E),(C1,C2),(C1,C3),(C1,C4),(C1,D),
(C1,E),(C2,C3),(C2,C4),(C2,D),(C2,E),(C3,C4),
(C3,D),(C3,E),(C4,D),(C4,E),(D,E),共28种可能.
其中恰好一个是合格品一个是次品的有:(C1,D),(C1,E),(C2,D),(C2,E),
(C3,D),(C3,E),(C4,D),(C4,E),共8种可能,
所以P=
=
.
故恰好一个是合格品一个是次品的概率为
.
a=1-0.15-0.35-0.15-0.25=0.1.
b=200-20-30-30-50=70.
(Ⅱ)由表可知:灯泡样品中优等品有50个,正品有100个,次品有50个,
∴优等品、正品和次品的比例为50:100:50=1:2:1.
∴按分层抽样法,购买灯泡数n=k+2k+k=4k(k∈N*),
∴n的最小值为4.
(Ⅲ)利用分层抽样在200个样品中抽取8个灯泡,每个等级抽取的个数分别为:
一等品的个数为8×
| 50 |
| 200 |
| 100 |
| 200 |
| 50 |
| 200 |
所以从一等品、合格品、次品分别抽取2个,4个,2个.
设一等品的2个为A、B,合格品的4个为C1、C2、C3、C4,次品的2个为D、E,
则从8个灯泡中随机抽取2个有:(A,B),(A,C1),(A,C2),(A,C3),
(A,C4),(A,D),(A,E),(B,C1),(B,C2),(B,C3),(B,C4),
(B,D),(B,E),(C1,C2),(C1,C3),(C1,C4),(C1,D),
(C1,E),(C2,C3),(C2,C4),(C2,D),(C2,E),(C3,C4),
(C3,D),(C3,E),(C4,D),(C4,E),(D,E),共28种可能.
其中恰好一个是合格品一个是次品的有:(C1,D),(C1,E),(C2,D),(C2,E),
(C3,D),(C3,E),(C4,D),(C4,E),共8种可能,
所以P=
| 8 |
| 28 |
| 2 |
| 7 |
故恰好一个是合格品一个是次品的概率为
| 2 |
| 7 |
点评:本题考查频率分布表的应用,考查分层抽样的应用,解题时要认真审题.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
若非零实数a,b,c成等差数列,则函数y=ax2+bx+
c的图象与x轴交点的个数为( )
| 1 |
| 4 |
| A、0 | B、1 | C、2 | D、1或2 |
下列4个正方体图形中,l是正方体的一条对角线,点M、N、P分别为其所在棱的中点,能得出直线l⊥面MNP的所有图形的序号是( )
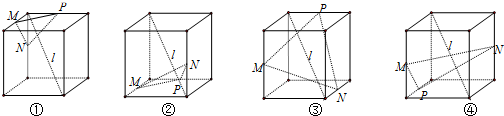

| A、①④ | B、①② | C、②④ | D、①③ |
数列0,
,
,
,
,…的通项公式为( )
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 5 |
| 2 |
| 3 |
A、an=
| ||
B、an=
| ||
C、an=
| ||
D、an=
|