题目内容
函数y=
+
的最小正周期是 .
| 1+sinx÷cosx |
| 1+sinx-cosx |
| 1+sinx-cosx |
| 1+sinx+cosx |
考点:三角函数中的恒等变换应用,三角函数的周期性及其求法
专题:三角函数的求值,三角函数的图像与性质
分析:首先利用三角函数的倍角公式对函数的关系式进行恒等变换,对函数的关系式进行化简,整理成只含有一个三角函数的形式,进一步利用函数的最小正周期的关系式求出结果.
解答:
解:y=
+
=
+
=
+
=
=
由于函数sinx的最小正周期:2π
所以:函数y=
+
的最小正周期为2π.
故答案为:2π
| 1+sinx+cosx |
| 1+sinx-cosx |
| 1+sinx-cosx |
| 1+sinx+cosx |
=
2sin
| ||||||
2sin
|
2sin
| ||||||
2sin
|
=
cos
| ||
sin
|
sin
| ||
cos
|
=
sin2
| ||||
sin
|
=
| 2 |
| sinx |
由于函数sinx的最小正周期:2π
所以:函数y=
| 1+sinx+cosx |
| 1+sinx-cosx |
| 1+sinx-cosx |
| 1+sinx+cosx |
故答案为:2π
点评:本题考查的知识要点:三角函数关系式的恒等变换,倍角公式的灵活应用,三角函数最小正周期的应用.属于基础题型.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案
相关题目
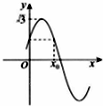 已知f(x)=Asin(2x+
已知f(x)=Asin(2x+
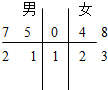 某校高三年级共有300人参加数学期中考试,从中随机抽取4名男生和4名女生的试卷,获得某一道题的样本,该题得分的茎叶图如图.
某校高三年级共有300人参加数学期中考试,从中随机抽取4名男生和4名女生的试卷,获得某一道题的样本,该题得分的茎叶图如图.