题目内容
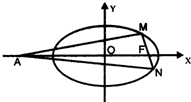 椭圆C:
椭圆C:| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 3 |
| MF |
| FN |
(Ⅰ)求椭圆C的方程;
(Ⅱ)当λ=1时,问:MN与AF是否垂直;并证明你的结论.
(Ⅲ)当M、N两点在C上运动,且
| AM |
| AN |
| 3 |
考点:直线与圆锥曲线的关系,椭圆的标准方程
专题:圆锥曲线的定义、性质与方程
分析:(I)利用椭圆C:
+
=1(a>b>0)过点P(
,1),且离心率为
,可得
=
,
+
=1.解出即可.
(II)设M(x1,y1),N(x2,y2),F(2,0),当λ=1时,
=
,可得-y1=y2,x1+x2=4,由M,N两点在椭圆上,可得
=6(1-
),
=6(1-
),可得x1=x2.即可得出.
(III)由
•
×tan∠MAN=2S△AMN=|AF||yM-yN|=6
及|AF|=6,可 得|yM-yN|=
.设直线MN的方程为:y=k(x-2),(k≠0),与椭圆的方程联立可得根与系数的关系即可得出.
| x2 |
| a2 |
| y2 |
| b2 |
| 3 |
| ||
| 3 |
1-(
|
| ||
| 3 |
| 3 |
| a2 |
| 1 |
| b2 |
(II)设M(x1,y1),N(x2,y2),F(2,0),当λ=1时,
| MF |
| FN |
| x | 2 1 |
| ||
| 2 |
| x | 2 2 |
| ||
| 2 |
(III)由
| AM |
| AN |
| 3 |
| 3 |
解答:
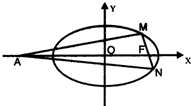 解:(Ⅰ)∵椭圆的离心率为e=
解:(Ⅰ)∵椭圆的离心率为e=
=
,
即
=
,可得
=
,
又椭圆C过点P(
),
∴
+
=1.
解得a2=6,b2=2,椭圆C的方程为
+
=1.①
(Ⅱ)设M(x1,y1),N(x2,y2),F(2,0),
则
=(2-x1,-y1),
=(x2-2,y2),
当λ=1时,
=
,∴-y1=y2,x1+x2=4,
由M,N两点在椭圆上,
∴
=6(1-
),
=6(1-
),
∴
=
.
若x1=-x2,则x1+x2=0≠2c=4(舍去),
∴x1=x2.
∴
=(0,2y2),
=(6,0),
∴
⊥
.
(Ⅲ)∵
•
×tan∠MAN=2S△AMN=|AF||yM-yN|=6
.
由已知点F(2,0),∴|AF|=6,
即得|yM-yN|=
.
当MN⊥x轴时,yM-yN≠
故直线的斜率存在.
不妨设直线MN的方程为:y=k(x-2),(k≠0),②
联立①②得(1+3k2)y2+4ky-2k2=0,
∴|yM-yN|=
=
,解得k=±1.
此时,直线MN的方程为x-y-2=0,或x+y-2=0.
 解:(Ⅰ)∵椭圆的离心率为e=
解:(Ⅰ)∵椭圆的离心率为e=| c |
| a |
| ||
| 3 |
即
1-(
|
| ||
| 3 |
| b2 |
| a2 |
| 1 |
| 3 |
又椭圆C过点P(
| 3,1 |
∴
| 3 |
| a2 |
| 1 |
| b2 |
解得a2=6,b2=2,椭圆C的方程为
| x2 |
| 6 |
| y2 |
| 2 |
(Ⅱ)设M(x1,y1),N(x2,y2),F(2,0),
则
| MF |
| NF |
当λ=1时,
| MF |
| FN |
由M,N两点在椭圆上,
∴
| x | 2 1 |
| ||
| 2 |
| x | 2 2 |
| ||
| 2 |
∴
| x | 2 1 |
| x | 2 2 |
若x1=-x2,则x1+x2=0≠2c=4(舍去),
∴x1=x2.
∴
| MN |
| AF |
∴
| MN |
| AF |
(Ⅲ)∵
| AM |
| AN |
| 3 |
由已知点F(2,0),∴|AF|=6,
即得|yM-yN|=
| 3 |
当MN⊥x轴时,yM-yN≠
| 3 |
不妨设直线MN的方程为:y=k(x-2),(k≠0),②
联立①②得(1+3k2)y2+4ky-2k2=0,
∴|yM-yN|=
| ||
| 1+3k2 |
| 3 |
此时,直线MN的方程为x-y-2=0,或x+y-2=0.
点评:本题考查了椭圆的标准方程及其性质、直线与椭圆相交问题转化为方程联立可得根与系数、弦长公式、三角形的面积计算公式、数量积运算,考查了推理能力与计算能力,考查了分类讨论的思想方法,属于难题.

练习册系列答案
相关题目
已知集合A={x|-1≤x≤2},B={x|x≤a},若A∩B≠∅,则实数a的取值范围为( )
| A、{a|a<2} |
| B、{a|a≥-1} |
| C、{a|a>-1} |
| D、{a|-1≤a<2} |
 若椭圆
若椭圆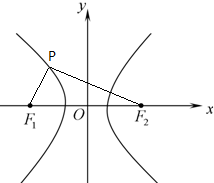 如图,若F1,F2是双曲线
如图,若F1,F2是双曲线