题目内容
当x<0时,函数y=x+
的最大值是 .
| 4 |
| x |
考点:基本不等式
专题:计算题,不等式的解法及应用
分析:由于x<0时,y=x+
=-[(-x)+
],再由基本不等式,即可得到最大值.
| 4 |
| x |
| 4 |
| -x |
解答:
解:当x<0时,y=x+
=-[(-x)+
]≤-2
=-4,
当且仅当x=-2取最大值-4.
故答案为:-4.
| 4 |
| x |
| 4 |
| -x |
(-x)•
|
当且仅当x=-2取最大值-4.
故答案为:-4.
点评:本题考查基本不等式及运用,注意运用求最值:需考虑一正二定三等,属于中档题和易错题.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
设全集U=R,集合A={x|x>1},B={x|x2-2x-3≥0},则A∩(∁UB)=( )
| A、{x|x≤-1} |
| B、{x|x≤1} |
| C、{x|-1<x≤1} |
| D、{x|1<x<3} |
设集合A={3,5,6,8},B={4,5,7,8},则A∩B=( )
| A、{5,8} |
| B、{7,8} |
| C、{5,3} |
| D、{4,6} |
已知函数f(x)=
,(a>0,a≠1).若数列{an}满足an=f(n)且an+1>an,n∈N*,则实数a的取值范围是( )
|
| A、(7,8) |
| B、[7,8) |
| C、(4,8) |
| D、(1,8) |
已知集合A={1,2,3}.则满足A∪B=A的非空集合B的个数是( )
| A、1 | B、2 | C、7 | D、8 |
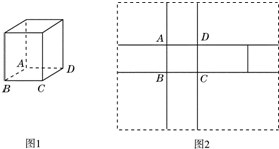 图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是
图2中的实线围成的部分是长方体(图1)的平面展开图,其中四边形ABCD是边长为1的正方形.若向虚线围成的矩形内任意抛掷一质点,它落在长方体的平面展开图内的概率是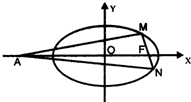 椭圆C:
椭圆C: