题目内容
若方程ax2+2x+1=0有且只有一个负根,则a的取值范围是 .
考点:函数的零点与方程根的关系,函数的零点
专题:计算题,分类讨论
分析:分别考虑二次项系数a=0,a≠0,利用二次方程的根与系数关系分别检验方程根的存在情况,可求a的范围.
解答:
解:(1)当a=0时,方程变为2x+1=0,可得x=-
,有且只有一个负根,故符合题意;
(2)当a<0时,∵f(0)=1>0,此时方程有且仅有一个负根,满足题意;
(3)当a>0时,f(0)=1>0,且△=4-4a,若△≥0,方程有两个负根,
若△<0,方程没有实数根.
综上可得,a的取值范围是 {a|a≤0}.
故答案为:{a|a≤0}.
| 1 |
| 2 |
(2)当a<0时,∵f(0)=1>0,此时方程有且仅有一个负根,满足题意;
(3)当a>0时,f(0)=1>0,且△=4-4a,若△≥0,方程有两个负根,
若△<0,方程没有实数根.
综上可得,a的取值范围是 {a|a≤0}.
故答案为:{a|a≤0}.
点评:本题主要考查了方程的根的存在情况的讨论,解题中不要漏掉a=0的情况,另外还要注意:方程有且只有一个负根与两个相等的负根的区别.

练习册系列答案
相关题目
过点P(1,1)的直线将圆形区域{(x,y)|x2+y2≤9}分成两部分,使得两部分的面积相差最大,则该直线的方程是( )
| A、x+y-2=0 |
| B、y-1=0 |
| C、x-y=0 |
| D、x+3y-4=0 |
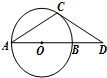 (几何证明选讲选做题)如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若
(几何证明选讲选做题)如图,已知点D在圆O直径AB的延长线上,过D作圆O的切线,切点为C.若