题目内容
6.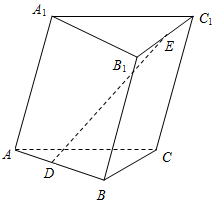 如图,点D,E分别是三棱柱ABC-A1B1C1的棱AB,B1C1的中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$.
如图,点D,E分别是三棱柱ABC-A1B1C1的棱AB,B1C1的中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$.(1)用向量$\overrightarrow{a}$,$\overrightarrow{b}$,$\overrightarrow{c}$表示向量$\overrightarrow{DE}$;
(2)已知向量$\overrightarrow{m}$是平面ACC1A1的一个法向量,利用$\overrightarrow{m}$与$\overrightarrow{DE}$的关系,证明:DE∥平面ACC1A1.
分析 (1)可取BC的中点F,并连接DF,EF,从而可以得到$\overrightarrow{DF}=\frac{1}{2}\overrightarrow{b},\overrightarrow{FE}=\overrightarrow{c}$,这样即可得出$\overrightarrow{DE}=\frac{1}{2}\overrightarrow{b}+\overrightarrow{c}$;
(2)根据法向量的概念,可以得到$\overrightarrow{m}⊥\overrightarrow{b},\overrightarrow{m}⊥\overrightarrow{c}$,从而得到$\overrightarrow{m}•\overrightarrow{b}=0,\overrightarrow{m}•\overrightarrow{c}=0$,这样即可求出$\overrightarrow{m}•\overrightarrow{DE}=0$,从而有$\overrightarrow{m}⊥\overrightarrow{DE}$,这便得出DE∥平面ACC1A1.
解答 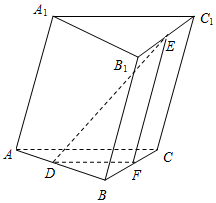 解:(1)如图,取BC中点F,连接DF,EF,则:
解:(1)如图,取BC中点F,连接DF,EF,则:
$\overrightarrow{DE}=\overrightarrow{DF}+\overrightarrow{FE}=\frac{1}{2}\overrightarrow{AC}+\overrightarrow{A{A}_{1}}$=$\frac{1}{2}\overrightarrow{b}+\overrightarrow{c}$;
(2)$\overrightarrow{m}$是平面ACC1A1的一个法向量;
∴$\overrightarrow{m}⊥\overrightarrow{b},\overrightarrow{m}⊥\overrightarrow{c}$;
∴$\overrightarrow{m}•\overrightarrow{b}=\overrightarrow{m}•\overrightarrow{c}=0$;
∴$\overrightarrow{m}•\overrightarrow{DE}=\overrightarrow{m}•(\frac{1}{2}\overrightarrow{b}+\overrightarrow{c})$=0;
∴$\overrightarrow{m}⊥\overrightarrow{DE}$;
又DE?平面ACC1A1;
∴DE∥平面ACC1A1.
点评 考查向量加法、数乘的几何意义,三角形中位线的性质,相等向量的概念,以及平面法向量的概念,向量垂直的充要条件,向量的数量积的运算.

 阅读快车系列答案
阅读快车系列答案| A. | $\frac{5\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{5}}{2}$ | C. | $\frac{\sqrt{37}}{2}$ | D. | $\frac{\sqrt{21}}{2}$ |
| A. | 16 | B. | 8 | C. | 4 | D. | 2 |