题目内容
14.已知空间向量$\vec a$=(1,n,2),$\vec b$=(-2,1,2),若2$\vec a$-$\vec b$与$\vec b$垂直,则|$\vec a$|等于( )| A. | $\frac{5\sqrt{3}}{2}$ | B. | $\frac{3\sqrt{5}}{2}$ | C. | $\frac{\sqrt{37}}{2}$ | D. | $\frac{\sqrt{21}}{2}$ |
分析 利用向量垂直关系,2$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直,则(2$\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$=0,即可得出.
解答 解:∵$\overrightarrow{a}$=(1,n,2),$\overrightarrow{b}$=(-2,1,2),
∴2$\overrightarrow{a}$-$\overrightarrow{b}$=(4,2n-1,2),
∵2$\overrightarrow{a}$-$\overrightarrow{b}$与$\overrightarrow{b}$垂直,
∴(2$\overrightarrow{a}$-$\overrightarrow{b}$)•$\overrightarrow{b}$=0,
∴-8+2n-1+4=0,
解得,n=$\frac{5}{2}$,
∴$\overrightarrow{a}$=(1,$\frac{5}{2}$,2)
∴|$\overrightarrow{a}$|=$\sqrt{{1}^{2}{+2}^{2}{+(\frac{5}{2})}^{2}}$=$\frac{3\sqrt{5}}{2}$.
故选:B.
点评 本题考查的知识点是向量的数量积判断向量垂直,其中根据两向量垂直数量积为0.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
5.若全集U={x|x2≤4},A={x|-2≤x≤0},则∁UA=( )
| A. | (0,2) | B. | [0,2) | C. | (0,2] | D. | [0,2] |
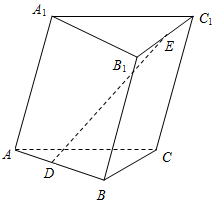 如图,点D,E分别是三棱柱ABC-A1B1C1的棱AB,B1C1的中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$.
如图,点D,E分别是三棱柱ABC-A1B1C1的棱AB,B1C1的中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$.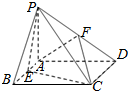 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,F是PD的中点,若$PA=AD=3,CD=\sqrt{6}$
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,F是PD的中点,若$PA=AD=3,CD=\sqrt{6}$