题目内容
18.设等比数列{an}的前n项积为Pn,若P12=32P7,则a10的值是( )| A. | 16 | B. | 8 | C. | 4 | D. | 2 |
分析 根据题意,利用等比数列的通项公式,得出a8•a9•…•a12=(a10)5=32,即可求出a10的值.
解答 解:∵等比数列{an}的前n项积为Pn,且P12=32P7,
∴a1•a2•a3•…•a12=32a1•a2•a3•…•a7,
即a8•a9•…•a12=32,
即(a10)5=32,
解得a10=2.
故选:D.
点评 本题考查了等比数列的性质与前n项积的应用问题,是基础题目.

练习册系列答案
相关题目
8.复数$\frac{{|{4+3i}|}}{3-4i}$(i为虚数单位)的共轭复数对应的点位于复平面内( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
13.已知函数f(x)=3-ax+1的图象恒过定点P,则点P的坐标是( )
| A. | (0,3) | B. | (-1,2) | C. | (-1,3) | D. | (3,-1) |
7.直三棱柱ABC-A1B1C1中,底面是正三角形,三棱柱的高为$\sqrt{3}$,若P是△A1B1C1中心,且三棱柱的体积为$\frac{9}{4}$,则PA与平面ABC所成的角大小是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
8.现有5人参加抽奖活动,每人依次从装有5张奖票(其中3张为中奖票)的箱子中不放回地随机抽取一张,直到3张中奖票都被抽出时活动结束,则活动恰好在第4人抽完结束的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
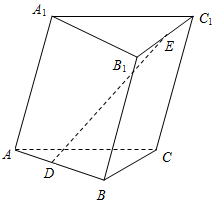 如图,点D,E分别是三棱柱ABC-A1B1C1的棱AB,B1C1的中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$.
如图,点D,E分别是三棱柱ABC-A1B1C1的棱AB,B1C1的中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$.