题目内容
16.已知数列{an}是等差数列,cn=an2-an+12(n∈N*)(1)判断数列{cn}是否为等差数列,并说明理由;
(2)如果a1+a3+…+a25=130,a2+a4+…+a26=117,试求数列{an}的公差d及通项公式.
分析 (1)通过已知条件及平方差公式计算即可.
(2)先求出公差,再根据等差数列的前n项和求出首项,再根据通项公式即可求出.
解答 解:(1)设数列{an}的公差为d,则an+2-an+1=an+1-an=d,
又∵cn=an2-an+12=-(a2n+1-an2)=-(an+1+an)(an+1-an),
∴cn+1-cn=-(an+2+an+1)(an+2-an+1)+(an+1+an)(an+1-an)
=-d[(an+2+an+1)-(an+1+an)]
=-d[(an+2-an+1)+(an+1-an)]
=-2d2,
故数列{cn}是以-2d2为公差的等差数列;
(2))∵a1+a3+…+a25=130,a2+a4+…+a26=117,
∴两式相减:13d=-13
∴d=-1,
∴13a1+$\frac{13×12}{2}$×2d=130,
∴a1=25
∴an=a1+(n-1)d=25+(n-1)×(-1)=26-n
点评 本题考查等差数列的判定,等差数列的前n项和公式,注意解题方法的积累,属于基础题

练习册系列答案
相关题目
7.直三棱柱ABC-A1B1C1中,底面是正三角形,三棱柱的高为$\sqrt{3}$,若P是△A1B1C1中心,且三棱柱的体积为$\frac{9}{4}$,则PA与平面ABC所成的角大小是( )
| A. | $\frac{π}{6}$ | B. | $\frac{π}{4}$ | C. | $\frac{π}{3}$ | D. | $\frac{2π}{3}$ |
11.函数f(x)=2tan(-x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 奇函数,也是偶函数 | D. | 非奇非偶函数 |
8.现有5人参加抽奖活动,每人依次从装有5张奖票(其中3张为中奖票)的箱子中不放回地随机抽取一张,直到3张中奖票都被抽出时活动结束,则活动恰好在第4人抽完结束的概率为( )
| A. | $\frac{1}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{2}{5}$ |
5.已知角α的终边在射线y=-$\frac{3}{4}$x(x>0)上,3sinα-4cosα的值是( )
| A. | $\frac{7}{5}$ | B. | -$\frac{7}{5}$ | C. | 5 | D. | -5 |
2.已知函数y=f(x)的图象与函数y=2x的图象关于直线y=x对称,则f(2)的值为( )
| A. | 1 | B. | $\sqrt{2}$ | C. | 2 | D. | 4 |
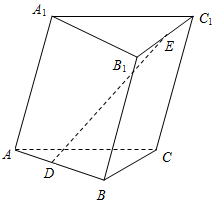 如图,点D,E分别是三棱柱ABC-A1B1C1的棱AB,B1C1的中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$.
如图,点D,E分别是三棱柱ABC-A1B1C1的棱AB,B1C1的中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$.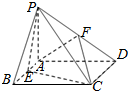 如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,F是PD的中点,若$PA=AD=3,CD=\sqrt{6}$
如图,四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD是矩形,F是PD的中点,若$PA=AD=3,CD=\sqrt{6}$