题目内容
16.设点M(x0,x0+$\sqrt{2}$),若在圆O:x2+y2=1上存在点N,使得∠OMN=45°,则X0的取值范围$[-\sqrt{2},0]$.分析 根据直线和圆的位置关系,利用数形结合即可得到结论.
解答  解:点M(x0,x0+$\sqrt{2}$)在直线y=x+$\sqrt{2}$上,与圆O:x2+y2=1相切,
解:点M(x0,x0+$\sqrt{2}$)在直线y=x+$\sqrt{2}$上,与圆O:x2+y2=1相切,
要使圆O:x2+y2=1上存在点N,使得∠OMN=45°,
则∠OMN的最大值大于或等于45°时,一定存在点N,使得∠OMN=45°,
而当MN与圆相切时∠OMN取得最大值,此时有MN=1,
∴x0的取值范围为$[-\sqrt{2},0]$.
故答案为:$[-\sqrt{2},0]$.
点评 本题考查直线与圆的位置关系,直线与直线设出角的求法,数形结合是快速解得本题的策略之一.

练习册系列答案
相关题目
11.下列命题中的说法正确的是( )
| A. | 命题“若x2=1,则x=1”的否命题为“若x2=1,则x≠1” | |
| B. | “x=-1”是“x2+5x-6=0”的必要不充分条件 | |
| C. | 命题“?x∈R,使得x2+x+1<0”的否定是:“?x∈R,均有x2+x+1>0” | |
| D. | 命题“在△ABC中,若A>B,则sinA>sinB”的逆否命题为真命题 |
8.复数$\frac{{|{4+3i}|}}{3-4i}$(i为虚数单位)的共轭复数对应的点位于复平面内( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
5.若全集U={x|x2≤4},A={x|-2≤x≤0},则∁UA=( )
| A. | (0,2) | B. | [0,2) | C. | (0,2] | D. | [0,2] |
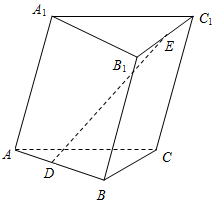 如图,点D,E分别是三棱柱ABC-A1B1C1的棱AB,B1C1的中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$.
如图,点D,E分别是三棱柱ABC-A1B1C1的棱AB,B1C1的中点,记$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{AC}$=$\overrightarrow{b}$,$\overrightarrow{A{A}_{1}}$=$\overrightarrow{c}$.