题目内容
18.若函数f(x)=$\left\{\begin{array}{l}{sin(2x-\frac{π}{6}),-π≤x<m}\\{cos(2x-\frac{π}{6}),m≤x≤\frac{π}{2}}\end{array}\right.$恰有4个零点,则m的取值范围为( )| A. | [-$\frac{11π}{12}$,-$\frac{π}{6}$]∪($\frac{π}{12}$,$\frac{π}{3}$] | B. | (-$\frac{11π}{12}$,-$\frac{2π}{3}$]∪(-$\frac{5π}{12}$,-$\frac{π}{6}$]∪($\frac{π}{12}$,$\frac{π}{3}$] | ||
| C. | [-$\frac{11π}{12}$,-$\frac{π}{6}$)∪[$\frac{π}{12}$,$\frac{π}{3}$) | D. | [-$\frac{11π}{12}$,-$\frac{2π}{3}$)∪[-$\frac{5π}{12}$,-$\frac{π}{6}$)∪[$\frac{π}{12}$,$\frac{π}{3}$) |
分析 设g(x)=sin(2x-$\frac{π}{6}$),h(x)=cos(2x-$\frac{π}{6}$),作出这两个函数在[-π,$\frac{π}{2}$]上的图象,求出零点,通过图象即可得到所求m的范围.
解答 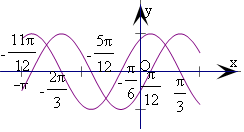 解:设g(x)=sin(2x-$\frac{π}{6}$),h(x)=cos(2x-$\frac{π}{6}$),
解:设g(x)=sin(2x-$\frac{π}{6}$),h(x)=cos(2x-$\frac{π}{6}$),
作出这两个函数在[-π,$\frac{π}{2}$]上的图象,如图所示:
g(x)在[-π,$\frac{π}{2}$]上的零点为-$\frac{11π}{12}$,-$\frac{5π}{12}$,$\frac{π}{12}$;
h(x)在[-π,$\frac{π}{2}$]上的零点为-$\frac{2π}{3}$,-$\frac{π}{6}$,$\frac{π}{3}$.
f(x)恰有4个零点,
由图象可得m∈(-$\frac{11π}{12}$,-$\frac{2π}{3}$]∪(-$\frac{5π}{12}$,-$\frac{π}{6}$]∪($\frac{π}{12}$,$\frac{π}{3}$].
故选:B.
点评 本题考查函数的零点个数问题解法,注意运用转化思想和数形结合思想方法,考查观察和判断能力,属于中档题.

练习册系列答案
相关题目
9.对命题“?x0∈R,x${\;}_{0}^{2}$-2x0+4>0”的否定正确的是( )
| A. | $?{x_0}∈R\;,\;{x_0}^2-2{x_0}+4>0$ | B. | ?x∈R,x2-2x+4≤0 | ||
| C. | ?x∈R,x2-2x+4>0 | D. | ?x∈R,x2-2x+4≥0 |
2.过点($\sqrt{2}$,0)引直线l与曲线y=$\sqrt{1-{x}^{2}}$相交于A,B两点,O为坐标原点,当△AOB的面积取最大值时,直线l的斜率等于( )
| A. | $\frac{\sqrt{3}}{3}$ | B. | -$\frac{\sqrt{3}}{3}$ | C. | ±$\frac{\sqrt{3}}{3}$ | D. | -$\sqrt{3}$ |
3.已知集合A={x|x<1},B={x|2x<1},则( )
| A. | A∩B={x|x<0} | B. | A∪B=R | C. | A∩B={x|x<1} | D. | A∪B={x|x<0} |