题目内容
曲线
的中心到直线y=
x的距离是( )
|
| ||
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
考点:参数方程化成普通方程
专题:计算题,坐标系和参数方程
分析:由参数方程可知其图象是以(1,0)为圆心,1为半径的圆,问题转化为圆心到直线的距离.
解答:
解:曲线
是以(1,0)为圆心,1为半径的圆,
则其中心为圆心(1,0),
则曲线
的中心到直线y=
x的距离为
=
.
故选A.
|
则其中心为圆心(1,0),
则曲线
|
| ||
| 3 |
|
| ||||
|
| 1 |
| 2 |
故选A.
点评:本题考查了常见参数方程的识别及点到直线的距离公式,属于基础题.

练习册系列答案
相关题目
函数y=f(x)为偶函数,且[0,+∞)上单调递减,则y=f(2-x2)的一个单调递增区间为( )
| A、(-∞,0] | ||
| B、[0,+∞) | ||
C、[0,
| ||
D、[
|
已知数列{an}满足 a1=1,an=1+
,则 a5=( )
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
在三角形ABC中A=
,AB=1,AC=2,设点P,Q满足
=λ
,
=(1-λ)
,若
•
=-2,λ=( )
| π |
| 2 |
| AP |
| AB |
| AQ |
| AC |
| BQ |
| CP |
A、
| ||
B、
| ||
C、
| ||
| D、2 |
如图给出的是计算
+
+
+…+
的值的一个程序框图,判断其中框内应填入的条件是( )

| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 20 |

| A、i>10 | B、i<10 |
| C、i>20 | D、i<20 |
已知α是锐角,则下列各式成立的是( )
A、sinα+cosα=
| ||
| B、sinα+cosα=1 | ||
C、sinα+cosα=
| ||
D、sinα+cosα=
|
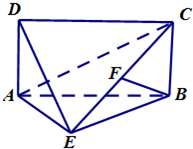 如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.
如图,四棱锥E-ABCD中,ABCD是矩形,平面EAB⊥平面ABCD,AE=EB=BC=2,F为CE上的点,且BF⊥平面ACE.