题目内容
已知α是锐角,则下列各式成立的是( )
A、sinα+cosα=
| ||
| B、sinα+cosα=1 | ||
C、sinα+cosα=
| ||
D、sinα+cosα=
|
考点:两角和与差的正弦函数
专题:计算题,三角函数的求值,三角函数的图像与性质
分析:由两角和的正弦公式得到sinα+cosα=
sin(α+
),再由α是锐角,求出1<sinα+cosα≤
.即可判断C正确.
| 2 |
| π |
| 4 |
| 2 |
解答:
解:由α是锐角,即0<α<
,
则sinα+cosα=
(
sinα+
cosα)=
sin(α+
),
由于
<α+
<
,
则
<sin(α+
)≤1.
即有1<sinα+cosα≤
.
则A,B,D错,C对.
故选C.
| π |
| 2 |
则sinα+cosα=
| 2 |
| ||
| 2 |
| ||
| 2 |
| 2 |
| π |
| 4 |
由于
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
则
| ||
| 2 |
| π |
| 4 |
即有1<sinα+cosα≤
| 2 |
则A,B,D错,C对.
故选C.
点评:本题考查两角和的正弦公式,正弦函数的性质,考查运算能力,属于中档题.

练习册系列答案
 芝麻开花课程新体验系列答案
芝麻开花课程新体验系列答案 怎样学好牛津英语系列答案
怎样学好牛津英语系列答案
相关题目
曲线
的中心到直线y=
x的距离是( )
|
| ||
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
已知
=(a,-2),
=(1,1-a),则“a=2”是“
∥
”的( )
| m |
| n |
| m |
| n |
| A、充要条件 |
| B、充分而不必要条件 |
| C、必要而不充分条件 |
| D、既不充分也不必要条件 |
设等差数列{an}的前n项和为Sn,已知(1-a2012)3+2014(1-a2012)=2014,(a3-1)3+2014(a3-1)=2014,则下列结论正确的是( )
| A、S2014=2014,a2012<a3 |
| B、S2014=2014,a2012>a3 |
| C、S2014=2013,a2012<a3 |
| D、S2014=2013,a2012>a3 |
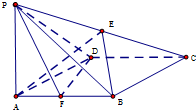 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠BAD=60°,AB=2,PA=1,PA⊥平面ABCD,E是PC的中点,F是AB的中点.