题目内容
正方体ABCD-A1B1C1D1中,异面直线AD与CB1所成的角为 .
考点:异面直线及其所成的角
专题:空间位置关系与距离
分析:正方体ABCD-A1B1C1D1中,由AD∥BC,可得异面直线AD与CB1所成角就是BC与CB1所成角,故∠BCB1 为异面直线AD与CB1所成角,解三角形可得答案.
解答:
解:∵正方体ABCD-A1B1C1D1中,AD∥BC,
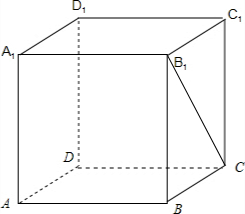
∴异面直线AD与CB1所成角就是BC与CB1所成角,
故∠BCB1 为异面直线AD与CB1所成角,
等腰直角三角形BCB1 中,
∠BCB1=45°,
故异面直线AD与CB1所成的角为45°,
故答案为:45°;

∴异面直线AD与CB1所成角就是BC与CB1所成角,
故∠BCB1 为异面直线AD与CB1所成角,
等腰直角三角形BCB1 中,
∠BCB1=45°,
故异面直线AD与CB1所成的角为45°,
故答案为:45°;
点评:本题考查的知识点是异面直线及其所成的角,其中找出∠BCB1 为异面直线AD与CB1所成角,是解答的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
的定义域是( )
| ||
| tanx |
A、{x|2kπ≤x≤2kπ+
| ||||
B、{x|2kπ<x<2kπ+
| ||||
| C、{x|2kπ<x<2kπ+π,k∈Z} | ||||
D、{x|2kπ-
|
等差数列{an}的前n项和为Sn,若a1+a3+a8=9,a6=9,则S9的值是( )
| A、64 | B、72 |
| C、54 | D、以上都不对 |
曲线
的中心到直线y=
x的距离是( )
|
| ||
| 3 |
A、
| ||||
B、
| ||||
| C、1 | ||||
D、
|
双曲线mx2-y2=1经过抛物线y2=2x的焦点,则m的值为( )
| A、4 | ||
| B、1 | ||
C、
| ||
D、
|
已知简谐振动f(x)=Asin(ωx+φ)(|φ|<
)的振幅为
,图象上相邻最高点与最低点之间的距离为5,且过点(0,
),则该简谐振动的频率与初相分别为( )
| π |
| 2 |
| 3 |
| 2 |
| 3 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|