题目内容
“?x＞0，x+1＞
”的否定是 ．
| x |
考点：命题的否定
专题：简易逻辑
分析：根据全称命题的否定是特称命题，即可得到结论．
解答：
解：根据全称命题的否定是特称命题可得命题的否定为?x＞0，x+1≤
，
故答案为：?x＞0，x+1≤
| x |
故答案为：?x＞0，x+1≤
| x |
点评：本题主要考查含有量词的命题的否定，比较基础．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=-x+log2
+1，则f（
）+f（-
）的值为（ ）
| 1-x |
| 1+x |
| 1 |
| 2 |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
| C、0 | ||
D、2log2
|
已知f（x）=ax3+bx-4其中a，b为常数，若f（-2）=7，则f（2）的值等于（ ）
| A、15 | B、-7 | C、14 | D、-15 |
函数f（x）=
的值域是（ ）
| 4-x2 |
| A、（0，2] |
| B、[0，2） |
| C、[0，2] |
| D、（-∞，2] |
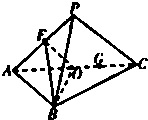如图，平面PAC⊥平面ABC，△ABC是以AC为斜边的等腰直角三角形，E，O分别为PA，AC的中点，AC=16，PA=PC=10．