题目内容
数列
，
，
，
，…，
的前n项和为 ．
| 3 |
| 2 |
| 9 |
| 4 |
| 25 |
| 8 |
| 65 |
| 16 |
| n•2n+1 |
| 2n |
考点：数列的求和
专题：等差数列与等比数列
分析：把数列的通项分解为
=n+
，分组后利用等差数列和等比数列的前n项和得答案．
| n•2n+1 |
| 2n |
| 1 |
| 2n |
解答：
解：∵
=n+
．
∴数列
，
，
，
，…，
的前n项和：
Sn=
+
+
+
+…+
=(1+
)+(2+
)+…+(n+
)
=(1+2+…+n)+(
+
+…+
)
=
+
=
+1-
=
-
．
故答案为：
-
．
| n•2n+1 |
| 2n |
| 1 |
| 2n |
∴数列
| 3 |
| 2 |
| 9 |
| 4 |
| 25 |
| 8 |
| 65 |
| 16 |
| n•2n+1 |
| 2n |
Sn=
| 3 |
| 2 |
| 9 |
| 4 |
| 25 |
| 8 |
| 65 |
| 16 |
| n•2n+1 |
| 2n |
=(1+
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
=(1+2+…+n)+(
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n |
=
| (1+n)n |
| 2 |
| ||||
1-
|
| n2+n |
| 2 |
| 1 |
| 2n |
=
| n2+n-2 |
| 2 |
| 1 |
| 2n |
故答案为：
| n2+n-2 |
| 2 |
| 1 |
| 2n |
点评：本题考查了数列的分组求和，考查了等差数列和等比数列的前n项和，是中档题．
练习册系列答案
相关题目
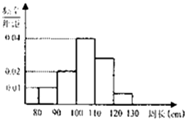为了解一片防风林的生长情况，随机测量了其中100株树木的底部周长（单位：cm）、根据所得数据画出样品的频率分布直方图（如图），那么在这100株树木中，底部周长大于100cm的株数是