题目内容
设f′(x)和g′(x)分别是f(x)和g(x)的导函数,若f′(x)g′(x)≤0在区间I上恒成立,则称f(x)和g(x)在区间I上单调性相反.若函数f(x)=
x3-2ax与g(x)=x2+2bx在开区间(a,b)上单调性相反(a>0),则b-a的最大值为( )
| 1 |
| 3 |
A、
| ||
| B、1 | ||
C、
| ||
| D、2 |
考点:函数的单调性与导数的关系
专题:导数的综合应用
分析:由条件知g′(x)>0恒成立,得f′(x)≤0恒成立,从而求出a、b的取值范围,建立b-a的表达式,求出最大值.
解答:
解:∵f(x)=
x3-2ax,g(x)=x2+2bx,
∴f′(x)=x2-2a,g′(x)=2x+2b;
由题意得f′(x)g′(x)≤0在(a,b)上恒成立,
∵a>0,∴b>a>0,∴2x+2b>0恒成立,
∴x2-2a≤0恒成立,即-
≤x≤
;
又∵0<a<x<b,∴b≤
,
即0<a≤
,解得0<a≤2;
∴b-a≤
-a=-(
-
)2+
,当a=
时,取“=”,
∴b-a的最大值为
.
故选:A.
| 1 |
| 3 |
∴f′(x)=x2-2a,g′(x)=2x+2b;
由题意得f′(x)g′(x)≤0在(a,b)上恒成立,
∵a>0,∴b>a>0,∴2x+2b>0恒成立,
∴x2-2a≤0恒成立,即-
| 2a |
| 2a |
又∵0<a<x<b,∴b≤
| 2a |
即0<a≤
| 2a |
∴b-a≤
| 2a |
| a |
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴b-a的最大值为
| 1 |
| 2 |
故选:A.
点评:本题考查了利用导数判定函数的单调性问题,也考查了不等式的解法问题,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
在平行四边形ABCD中,点E为CD中点,
=
,
=
,则
等于( )
| AB |
| a |
| AD |
| b |
| BE |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
椭圆
+
=1的焦点是F1,F2,如果椭圆上一点P满足PF1⊥PF2,下面结论正确的是( )
| x2 |
| 25 |
| y2 |
| 16 |
| A、P点有两个 |
| B、P点有四个 |
| C、P点不一定存在 |
| D、P点一定不存在 |
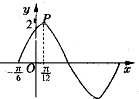 已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,
已知函数f(x)=2sin(ωx+φ),(ω>0,φ∈(0,