题目内容
在平面直角坐标系中,O是坐标原点,两定点A,B满足|
|=|
|=
•
=2,则点集{P|
=x
+y
,|x|+|y|≤1,x,y∈R}所表示的区域的面积是 .
| OA |
| OB |
| OA |
| OB |
| OP |
| OA |
| OB |
考点:平面向量的基本定理及其意义
专题:平面向量及应用
分析:由|
|=|
|=
•
=2,
=x
+y
,不妨设
=(2,0),
=(m,n),利用
=2,2m=2,
解得m=1,n=
.可得
=x
+y
=(2x+y,
y).令a=2x+y,b=
y,解得y=
,x=
a-
b,
由|x|+|y|≤1,x,y∈R,可得|
a-
b|+
|b|≤1,对a,b分类讨论,画出图形,可得(a,b)满足的区域为图中阴影部分.即可得出.
| OA |
| OB |
| OA |
| OB |
| OP |
| OA |
| OB |
| OA |
| OB |
| m2+n2 |
解得m=1,n=
| 3 |
| OP |
| OA |
| OB |
| 3 |
| 3 |
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
由|x|+|y|≤1,x,y∈R,可得|
| 1 |
| 2 |
| ||
| 6 |
| ||
| 3 |
解答:
解:∵|
|=|
|=
•
=2,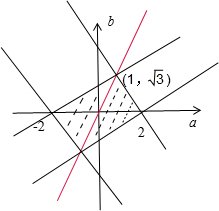
不妨设
=(2,0),
=(m,n),
∴
=2,2m=2,
解得m=1,n=
.
∵
=x
+y
,=x(2,0)+y(1,
)=(2x+y,
y).
令a=2x+y,b=
y,
解得y=
,x=
a-
b,
由|x|+|y|≤1,x,y∈R,可得|
a-
b|+
|b|≤1,
对a,b分类讨论,画出图形,可得(a,b)满足的区域为图中阴影部分.
可得(a,b)满足的区域的面积为4×
×2×
=4
.
故答案为:4
.
| OA |
| OB |
| OA |
| OB |

不妨设
| OA |
| OB |
∴
| m2+n2 |
解得m=1,n=
| 3 |
∵
| OP |
| OA |
| OB |
| 3 |
| 3 |
令a=2x+y,b=
| 3 |
解得y=
| ||
| 3 |
| 1 |
| 2 |
| ||
| 6 |
由|x|+|y|≤1,x,y∈R,可得|
| 1 |
| 2 |
| ||
| 6 |
| ||
| 3 |
对a,b分类讨论,画出图形,可得(a,b)满足的区域为图中阴影部分.
可得(a,b)满足的区域的面积为4×
| 1 |
| 2 |
| 3 |
| 3 |
故答案为:4
| 3 |
点评:本题考查了向量的运算性质、基本不等式的性质、线性规划的有关知识、的面积,考查了推理能力和计算能力,属于难题.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
已知函数y=2sinwx的图象与直线y+2=0的相邻两个公共点之间的距离为
,则w的值为( )
| 2π |
| 3 |
| A、3 | ||
B、
| ||
C、
| ||
D、
|
 如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1和AB上的点,则下列说法正确的是
如图,正方体ABCD-A1B1C1D1的棱长为1,E,F分别为棱DD1和AB上的点,则下列说法正确的是