题目内容
2.“x>0,y>0”是“$\frac{y}{x}+\frac{x}{y}≥2$”的( )| A. | 充分而不必要条件 | B. | 必要而不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分也不必要条件 |
分析 “x>0,y>0”?“$\frac{y}{x}+\frac{x}{y}≥2$”,反之不成立,例如取x=y=-1.
解答 解:“x>0,y>0”?“$\frac{y}{x}+\frac{x}{y}≥2$”,反之不成立,例如取x=y=-1.
∴x>0,y>0”是“$\frac{y}{x}+\frac{x}{y}≥2$”的充分而不必要条件.
故选:A.
点评 本题考查了基本不等式的性质、简易逻辑的判定方法,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阳光课堂课时作业系列答案
阳光课堂课时作业系列答案
相关题目
12.已知函数f(x)的导函数f′(x),满足(x-1)[xf′(x)-f(x)]>0,则下列关于f(x)的命题正确的是( )
| A. | f(3)<f(-3) | B. | f(2)>f(-2) | C. | f(3)<f(2) | D. | 2f(3)>3f(2) |
13.已知实数x,y满足$\left\{\begin{array}{l}{3x-y-7≥0}\\{5x-4y≤0}\\{y≤10}\end{array}\right.$,则$\frac{y+x}{x}$的最大值为( )
| A. | 1 | B. | $\frac{30}{17}$ | C. | $\frac{47}{17}$ | D. | 2 |
17.已知函数$f(x)=sin(ωx+\frac{π}{6})(ω>0)$的最小正周期为4π,则( )
| A. | 函数f(x)的图象关于原点对称 | |
| B. | 函数f(x)的图象关于直线$x=\frac{π}{3}$对称 | |
| C. | 函数f(x)图象上的所有点向右平移$\frac{π}{3}$个单位长度后,所得的图象关于原点对称 | |
| D. | 函数f(x)在区间(0,π)上单调递增 |
7.已知等比数列{an}为递增数列,Sn是其前n项和.若a1+a5=$\frac{17}{2}$,a2a4=4,则S6=( )
| A. | $\frac{27}{16}$ | B. | $\frac{27}{8}$ | C. | $\frac{63}{4}$ | D. | $\frac{63}{2}$ |
19.已知复数z1=2+6i,z2=-2i,若z1,z2在复平面内对应的点分别为A,B,线段AB的中点C对应的复数为z,则|z|=( )
| A. | $\sqrt{5}$ | B. | 5 | C. | 2$\sqrt{5}$ | D. | 2$\sqrt{17}$ |
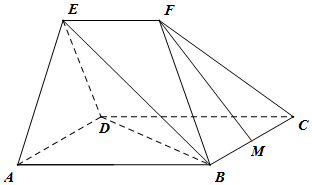 如图,在几何体ABCDEF中,平面ADE⊥平面ABCD,四边形ABCD为菱形,且∠DAB=60°,EA=ED=AB=2EF,EF∥AB,M为BC中点.
如图,在几何体ABCDEF中,平面ADE⊥平面ABCD,四边形ABCD为菱形,且∠DAB=60°,EA=ED=AB=2EF,EF∥AB,M为BC中点.