题目内容

19．已知复数z1=2+6i，z2=-2i，若z1，z2在复平面内对应的点分别为A，B，线段AB的中点C对应的复数为z，则|z|=（　　）
A．$\sqrt{5}$B．5C．2$\sqrt{5}$D．2$\sqrt{17}$

分析 复数z1=2+6i，z2=-2i，若z1，z2在复平面内对应的点分别为A（2，6），B（0，-2），利用中点坐标公式可得：线段AB的中点C（1，2）．进而得出．

解答 解：复数z1=2+6i，z2=-2i，若z1，z2在复平面内对应的点分别为A（2，6），B（0，-2），
线段AB的中点C（1，2）对应的复数为z=1+2i，则|z|=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$．
故选：A．

点评 本题考查了复数的运算法则、几何意义、中点坐标公式、模的计算公式，考查了推理能力与计算能力，属于基础题．

练习册系列答案
相关题目
2．“x＞0，y＞0”是“$\frac{y}{x}+\frac{x}{y}≥2$”的（　　）
A．充分而不必要条件B．必要而不充分条件
C．充分必要条件D．既不充分也不必要条件
3．已知直线$l：\left\{\begin{array}{l}x=2+\frac{{\sqrt{2}}}{2}t\\ y=\frac{{\sqrt{2}}}{2}t\end{array}\right.（t$为参数），曲线$C：\left\{\begin{array}{l}x=cosθ\\ y=sinθ\end{array}\right.（θ$为参数）．
（1）使判断l与C的位置关系；
（2）若把曲线C1上个点的横坐标压缩为原来的$\frac{1}{2}$倍，纵坐标压缩为原来的$\frac{{\sqrt{3}}}{2}$倍，得到曲线C2，设点P是曲线C2上一个动点，求它到直线l的距离的最小值．
7．已知等轴双曲线C的一个焦点是F1（-6，0），点M是等轴双曲线的渐近线上的一个动点，点P是圆（x+6）2+y2=1上的任意一点，则|PM|的最小值是（　　）
A．3$\sqrt{2}$-1B．2$\sqrt{3}$-1C．3$\sqrt{3}$+1D．2$\sqrt{3}$+2
14．设等差数列{an}的前n项和为Sn，Sm-1=13，Sm=0，Sm+1=-15．其中m∈N*且m≥2，则数列{$\frac{1}{{a}_{n}{a}_{n+1}}$}的前n项和的最大值为（　　）
A．$\frac{24}{143}$B．$\frac{1}{143}$C．$\frac{24}{13}$D．$\frac{6}{13}$
4．已知实数x，y满足$\left\{\begin{array}{l}{2x-y+6≥0}\\{x+y≥0}\\{x≤2}\end{array}\right.$，若目标函数z=-mx+y的最大值为-2m+10，最小值为-2m-2，则实数m的取值不可能是（　　）
A．3B．2C．0D．-1
11．已知函数g（x）=lnx-ax2+（2-a）x，a∈R．
（1）求g（x）的单调区间；
（2）若函数f（x）=g（x）+（a+1）x2-2x，x1，x2（x1＜x2）是函数f（x）的两个零点，f′（x）是函数f（x）的导函数，证明：f′（$\frac{{x}_{1}+{x}_{2}}{2}$）＜0．
8．在△ABC中，角A、B、C所对的边分别为a，b，c，满足（2a-c）cosB=bcosC．
（1）求B的大小；
（2）如图，AB=AC，在直线AC的右侧取点D，使得AD=2CD=4．当角D为何值时，四边形ABCD面积最大．
9．某程序框图如图所示，则该程序运行后输出的值是（　　）
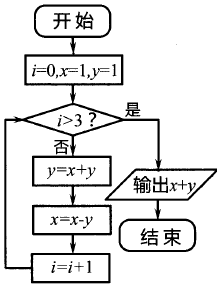
A．0B．-1C．-2D．-8

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网