题目内容
已知数列{an}满足奇数项a1,a3,a5,…成等差数列{a2n-1}(n∈N+),而偶数项a2,a4,a6,…成等比数列{a2n}(n∈N+),且a1=1,a2=2,a2,a3,a4,a5成等差数列,数列{an}的前n项和为Sn.
(Ⅰ)求通项an;
(Ⅱ)求Sn.
(Ⅰ)求通项an;
(Ⅱ)求Sn.
考点:数列的求和
专题:等差数列与等比数列
分析:(Ⅰ)先利用等差数列及等比数列的定义求得a2n-1=2n-1,a2n=2n,进而分n为奇数和偶数写出an.
(Ⅱ)利用等差数列及等比数列的求和公式分别求得奇数项的和及偶数项的和,即得结论.
(Ⅱ)利用等差数列及等比数列的求和公式分别求得奇数项的和及偶数项的和,即得结论.
解答:
解:(Ⅰ)设等差数列{a2n-1}(n∈N+)的公差为d,等比数列{a2n}(n∈N+)的公比为q,
则2(1+d)=2+2q,4q=(1+d)+(1+2d),解得q=d=2.…(3分)
于是a2n-1=2n-1,a2n=2n,即数列的通项an=
…(6分)
(Ⅱ)于是当n为偶数时,数列奇数项的和为[
]×
=
,
偶数项的和为
=2
+1-2,故Sn=
+2
+1-2.…(10分)
当n为奇数时,Sn=Sn-1+an=
+2
-2+n=2
+
.
于是Sn=
…(13分)
则2(1+d)=2+2q,4q=(1+d)+(1+2d),解得q=d=2.…(3分)
于是a2n-1=2n-1,a2n=2n,即数列的通项an=
|
(Ⅱ)于是当n为偶数时,数列奇数项的和为[
1+(2×
| ||
| 2 |
| n |
| 2 |
| n2 |
| 4 |
偶数项的和为
2(1-2
| ||
| 1-2 |
| n |
| 2 |
| n2 |
| 4 |
| n |
| 2 |
当n为奇数时,Sn=Sn-1+an=
| (n-1)2 |
| 4 |
| n+1 |
| 2 |
| n+1 |
| 2 |
| n2+2n-7 |
| 4 |
于是Sn=
|
点评:本题主要考查等差数列、等比数列的定义性质及前n项和公式等知识,考查分类讨论思想运用及运算能力,属中档题.

练习册系列答案
相关题目
已知f(x)是定义在R上的函数,命题p:f(x)满足?x∈R,f(-x)=-f(x),命题q:f(0)=0,则命题p是命题q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分又不必要条件 |
△ABC的三个内角A,B,C的对边分别为a,b,c,已知sinB=1,向量
=(a,b),
=(1,2),若
∥
,则角A的大小为( )
| p |
| q |
| p |
| q |
A、
| ||
B、
| ||
C、
| ||
D、
|
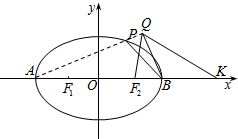 椭圆C:
椭圆C: