题目内容
已知函数y=f(x)是定义在R上的奇函数,对?x∈R都有f(x-1)=f(x+1)成立,当x∈(0,1]且x1≠x2时,有
<0.给出下列命题:
(1)f(1)=0
(2)f(x)在[-2,2]上有3个零点
(3)(2014,0)是函数y=f(x)的一个对称中心
(4)直线x=1是函数y=f(x)图象的一条对称轴.
其中正确命题的编号为 .
| f(x2)-f(x1) |
| x2-x1 |
(1)f(1)=0
(2)f(x)在[-2,2]上有3个零点
(3)(2014,0)是函数y=f(x)的一个对称中心
(4)直线x=1是函数y=f(x)图象的一条对称轴.
其中正确命题的编号为
考点:命题的真假判断与应用
专题:函数的性质及应用,简易逻辑
分析:根据函数奇偶性和周期性,单调性之间的关系,分别进行判断即可得到结论.
解答:
解:∵函数y=f(x)是定义在R上的奇函数,对?x∈R都有f(x-1)=f(x+1)成立,
令x=0,则f(-1)=f(1)=-f(1),解得f(1)=0.故(1)正确.
(2)∵f(x-1)=f(x+1)
∴f(x+2)=f(x),即函数的周期为2,
∵f(0)=f(2)=f(-2),f(-1)=f(1),∴f(x)在[-2,2]上至少有5个零点,故(2)错误.
(3)∵函数的周期为2,
∴f(2014)=f(0)=0,即(2014,0)是函数y=f(x)的一个对称中心,故(3)正确.
(4)∵f(1)=0,∴(1,0)是函数的一个对称中心,
∵当x∈(0,1]且x1≠x2时,有
<0.
∴此时函数单调递减,
∴x=1不是函数y=f(x)图象的一条对称轴,故(4)错误,
故正确的命题是(1)(3),
故答案为:(1)(3)
令x=0,则f(-1)=f(1)=-f(1),解得f(1)=0.故(1)正确.
(2)∵f(x-1)=f(x+1)
∴f(x+2)=f(x),即函数的周期为2,
∵f(0)=f(2)=f(-2),f(-1)=f(1),∴f(x)在[-2,2]上至少有5个零点,故(2)错误.
(3)∵函数的周期为2,
∴f(2014)=f(0)=0,即(2014,0)是函数y=f(x)的一个对称中心,故(3)正确.
(4)∵f(1)=0,∴(1,0)是函数的一个对称中心,
∵当x∈(0,1]且x1≠x2时,有
| f(x2)-f(x1) |
| x2-x1 |
∴此时函数单调递减,
∴x=1不是函数y=f(x)图象的一条对称轴,故(4)错误,
故正确的命题是(1)(3),
故答案为:(1)(3)
点评:本题主要考查与函数性质有关的命题的真假判断,涉及函数的奇偶性,周期性,单调性和对称性,综合考查函数的性质的综合应用.

练习册系列答案
相关题目
已知集合A={1,2,3},B={1,2,4},则A∩B等于( )
| A、{1,2,4} |
| B、{2,3,4} |
| C、{1,2} |
| D、{1,2,3,4} |
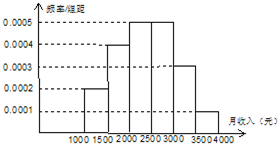 一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)/月收入段应抽出
一个社会调查机构就某地居民的月收入调查了10000人,并根据所得数据画了样本的频率分布直方图(如图).为了分析居民的收入与年龄、学历、职业等方面的关系,要从这10000人中再用分层抽样方法抽出100人作进一步调查,则在[2500,3000)(元)/月收入段应抽出