题目内容
已知f(x)=2ax+blnx-1,设曲线y=f(x)在点(1,f(1))处的切线为y=0.
(Ⅰ)求实数a,b的值;
(Ⅱ)设函数g(x)=mf(x)+
-mx.
(i)若m∈R,求函数g(x)的单调区间;
(ii)若1<m<3,求证:当x∈[1,e]时,g(x)<
-2.
(Ⅰ)求实数a,b的值;
(Ⅱ)设函数g(x)=mf(x)+
| x2 |
| 2 |
(i)若m∈R,求函数g(x)的单调区间;
(ii)若1<m<3,求证:当x∈[1,e]时,g(x)<
| e2 |
| 2 |
考点:导数在最大值、最小值问题中的应用,利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:(Ⅰ)由已知f′(x)=2a+
,依题意f(1)=0,且f'(1)=0,由此能求出实数a,b的值.
(Ⅱ)(i)由f(x)=x-lnx-1,x>0,得g(x)=
-mlnx-m(x>0),g′(x)=x-
=
,由此能求出函数g(x)的单调区间.
(ii)当1<m<3,x∈[1,e]时,
∈[1,e],g(x)在区间[1,
)上是减函数,在区间(
,e]上是增函数,由此能证明x∈[1,e]时,g(x)<
-2.
| b |
| x |
(Ⅱ)(i)由f(x)=x-lnx-1,x>0,得g(x)=
| x2 |
| 2 |
| m |
| x |
| x2-m |
| x |
(ii)当1<m<3,x∈[1,e]时,
| m |
| m |
| m |
| e2 |
| 2 |
解答:
解:(Ⅰ)由已知f′(x)=2a+
,
依题意f(1)=0,且f'(1)=0
所以
,
解得a=
,b=-1…(5分)
(Ⅱ)(i)由(Ⅰ)得f(x)=x-lnx-1,x>0
所以g(x)=
-mlnx-m(x>0),g′(x)=x-
=
…(6分)
当m≤0,g'(x)≥0在(0,+∞)上恒成立,
所以在区间(0,+∞)上是增函数,…(7分)
当m>0时,由g'(x)>0得x>
,由g'(x)<0得0<x<
,
所以g(x)在区间(0,
)上是减函数,在区间(
,+∞)上是增函数,…(9分)
(ii)当1<m<3,x∈[1,e]时,
∈[1,e],
g(x)在区间[1,
)上是减函数,在区间(
,e]上是增函数
所以g(x)最大值为max(g(1),g(e))…(11分)
又因为1<m<3,g(e)=
-2m<
-2,g(1)=
-m<0<
-2
所以当1<m<3,x∈[1,e]时,g(x)<
-2…(14分)
| b |
| x |
依题意f(1)=0,且f'(1)=0
所以
|
解得a=
| 1 |
| 2 |
(Ⅱ)(i)由(Ⅰ)得f(x)=x-lnx-1,x>0
所以g(x)=
| x2 |
| 2 |
| m |
| x |
| x2-m |
| x |
当m≤0,g'(x)≥0在(0,+∞)上恒成立,
所以在区间(0,+∞)上是增函数,…(7分)
当m>0时,由g'(x)>0得x>
| m |
| m |
所以g(x)在区间(0,
| m |
| m |
(ii)当1<m<3,x∈[1,e]时,
| m |
g(x)在区间[1,
| m |
| m |
所以g(x)最大值为max(g(1),g(e))…(11分)
又因为1<m<3,g(e)=
| e2 |
| 2 |
| e2 |
| 2 |
| 1 |
| 2 |
| e2 |
| 2 |
所以当1<m<3,x∈[1,e]时,g(x)<
| e2 |
| 2 |
点评:本题考查实数的求法,考查函数的单调性的求法,考查不等式的证明,解题时要认真审题,注意导数性质的合理运用.

练习册系列答案
 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案
相关题目
已知函数f(x)=-x3+bx2-
b3(b>0),有且仅有两个不同的零点x1,x2,则( )
| 4 |
| 27 |
| A、x1+x2>0,x1x2<0 |
| B、x1+x2>0,x1x2>0 |
| C、x1+x2<0,x1x2<0 |
| D、x1+x2<0,x1x2>0 |
已知a,b,c,d是四条不重合的直线,其中c为a在平面α上的射影,d为b在平面α上的射影,则( )
| A、c∥d⇒a∥b |
| B、a⊥b⇒c⊥d |
| C、a∥b⇒c∥d |
| D、c⊥d⇒a⊥b |
定义在R上的函数f(x)满足f(x)=
,则f(2015)=( )
|
| A、-1 | B、0 | C、1 | D、2 |
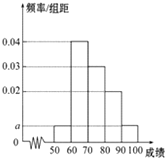 某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]
某校100名学生期中考试语文成绩的频率分布直方图如图所示,其中成绩分组区间是:[50,60),[60,70),[70,80),[80,90),[90,100]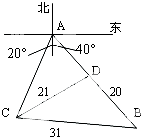 观测站C处在目标A的南偏西20°方向,从A出发有一条南偏东40°走向的公路,在C处观测到与C相距31km公路上的B处有一人正沿此公路向A走去,走20km到达D处,此时测得CD距离21km,求此人在D处距A还有多远?
观测站C处在目标A的南偏西20°方向,从A出发有一条南偏东40°走向的公路,在C处观测到与C相距31km公路上的B处有一人正沿此公路向A走去,走20km到达D处,此时测得CD距离21km,求此人在D处距A还有多远?