题目内容
已知二次函数f(x)满足条件f(0)=0和f(x+2)-f(x)=4x
(1)求f(x);
(2)求f(x)在区间[a,a+2](a∈R)上的最小值g(a).
(1)求f(x);
(2)求f(x)在区间[a,a+2](a∈R)上的最小值g(a).
考点:二次函数的性质
专题:函数的性质及应用
分析:(1)先设出函数的表达式,由f(x+2)-f(x)=4x得方程组求出a,b的值即可;(2)通过讨论a的范围,根据函数的单调性,从而求出函数的最小值.
解答:
解:(1)∵f(0)=0,
∴设f(x)=ax2+bx,
∴a(x+2)2+b(x+2)-ax2-bx=4ax+4a+2b=4x,
∴
,解得:a=1,b=-2,
∴f(x)=x2-2x.
(2)当a+2≤1时,即a≤-1时,f(x)min=f(a+2)=a2+2a,
当a<1<a+2时,即-1<a<-1时,f(x)min=f(1)=-1
当a≥1时,f(x)min=a2-2a,
∴g(a)=
.
∴设f(x)=ax2+bx,
∴a(x+2)2+b(x+2)-ax2-bx=4ax+4a+2b=4x,
∴
|
∴f(x)=x2-2x.
(2)当a+2≤1时,即a≤-1时,f(x)min=f(a+2)=a2+2a,
当a<1<a+2时,即-1<a<-1时,f(x)min=f(1)=-1
当a≥1时,f(x)min=a2-2a,
∴g(a)=
|
点评:本题考查了求函数的表达式,考查二次函数的性质,函数的单调性,考查分类讨论思想,是一道中档题.

练习册系列答案
相关题目
(1)若函数f(x)=2x2-ax-1在(0,1)内存在x0,使得f(x0)=0,求a的取值范围.
(2)方程mx2+2(m+3)x+2m+14=0有两相异实根,一个大于4,一个小于4,求m的取值范围.
(2)方程mx2+2(m+3)x+2m+14=0有两相异实根,一个大于4,一个小于4,求m的取值范围.
已知函数f(x)=-x3+bx2-
b3(b>0),有且仅有两个不同的零点x1,x2,则( )
| 4 |
| 27 |
| A、x1+x2>0,x1x2<0 |
| B、x1+x2>0,x1x2>0 |
| C、x1+x2<0,x1x2<0 |
| D、x1+x2<0,x1x2>0 |
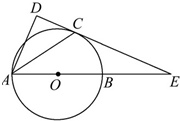 如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.
如图,已知AB是⊙O的直径,锐角∠DAB的平分线AC交⊙O于点C,作CD⊥AD,垂足为D,直线CD与AB的延长线交于点E.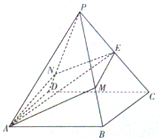 如图,正四棱锥P-ABCD的高为3,底面边长为2,E是棱PC的中点,过AE作平面与棱PB、PD分别交于点M、N(M、N可以是棱的端点).
如图,正四棱锥P-ABCD的高为3,底面边长为2,E是棱PC的中点,过AE作平面与棱PB、PD分别交于点M、N(M、N可以是棱的端点).