题目内容
5.已知函数f(x)=acosx+x2,x∈(-$\frac{π}{2}$,$\frac{π}{2}$),a∈R.(Ⅰ)若曲线y=f(x)在点($\frac{π}{6}$,f($\frac{π}{6}$))处的切线的斜率为$\frac{1}{2}+\frac{π}{3}$,求曲线y=f(x)在点(0,f(0))处的切线方程;
(Ⅱ)若f(x)≥2恒成立,求a的取值范围.
分析 (Ⅰ)根据导数的几何意义即可求出曲线y=f(x)在点(0,f(0))处的切线方程,
(Ⅱ)分离参数,构造函数,利用导数,求出函数最大值即可.
解答 解:(Ⅰ)∵函数f(x)=acosx+x2,x∈(-$\frac{π}{2}$,$\frac{π}{2}$),a∈R,
∴f′(x)=-asinx+2x,
∴f′($\frac{π}{6}$)=-asin$\frac{π}{6}$+$\frac{π}{3}$=-$\frac{1}{2}$a+$\frac{π}{3}$=$\frac{1}{2}+\frac{π}{3}$,
∴a=-1,
∴f′(0)=sin0+0=0,f(0)=-1,
∴线y=f(x)在点(0,f(0))处的切线方程y=-1,
(Ⅱ)∵f(x)≥2恒成立,
∴acosx+x2≥2,在x∈(-$\frac{π}{2}$,$\frac{π}{2}$)上恒成立,
∵0<cosx≤1
∴a≥$\frac{2-{x}^{2}}{cosx}$,
设g(x)=$\frac{2-{x}^{2}}{cosx}$,
∴g′(x)=$\frac{-2xcosx+(2-{x}^{2})sinx}{co{s}^{2}x}$,
令h(x)=-2xcosx+(2-x2)sinx,
∴h′(x)=-2cosx+2xsinx-2xsinx+(2-x2)cosx=-x2cosx<0,在(-$\frac{π}{2}$,$\frac{π}{2}$)上恒成立,
∴h(x)在(-$\frac{π}{2}$,$\frac{π}{2}$)单调递减,
∵h(-$\frac{π}{2}$)=-2+$\frac{{π}^{2}}{4}$>0,h(0)=0,h($\frac{π}{2}$)=2-$\frac{{π}^{2}}{4}$<0
∴当x∈(-$\frac{π}{2}$,0)时,g′(x)>0,函数g(x)单调递增,
当x∈(0,$\frac{π}{2}$)时,g′(x)<0,函数g(x)单调递减,
∴g(x)max=g(0)=2,
∴a≥2
点评 本题考查函数恒成立问题,考查导数知识的运用,考查学生的计算能力,考查分类讨论、转化与化归解题思想及其相应的运算能力.

 阅读快车系列答案
阅读快车系列答案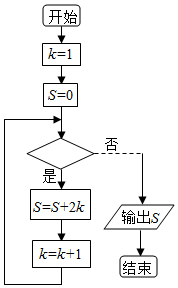 如果执行如图的程序框图,输出的S=30,则判断框处为( )
如果执行如图的程序框图,输出的S=30,则判断框处为( )| A. | k<5 | B. | k≤5 | C. | k≥6 | D. | k>6 |
| A. | -1 | B. | 1 | C. | -2 | D. | 2 |
| A. | -4 | B. | -1 | C. | 2 | D. | 5 |
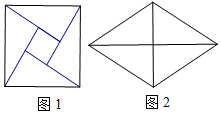 中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )
中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )| A. | $\frac{24}{25}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{25}$ |
| A. | (0,1) | B. | (0,2) | C. | (1,2) | D. | (2,+∞) |