题目内容
15.已知向量$\overrightarrow{m}$=($\sqrt{3}$cosωx,cosωx),$\overrightarrow{n}$=(sinωx,cosωx)(ω>0),函数f(x)=$\overrightarrow{m}$•$\overrightarrow{n}$的最小正周期为π.(Ⅰ)求ω的值及函数f(x)的单调递增区间;
(Ⅱ)在钝角△ABC中,角A,B,C所对的边分别为a,b,c,已知a=1,b=$\sqrt{3}$,当f(A)取得最大值时,求边c.
分析 (I)根据平面向量的数量积公式得出f(x)的解析式,利用三角恒等变换化简,根据周期公式计算ω,根据正弦函数的单调性列不等式求出单调增区间;
(II)求出A,根据正弦定理计算B,从而得出C,在计算c即可.
解答 解:(I)f(x)=$\sqrt{3}$cosωxsinωx+cos2ωx=$\frac{\sqrt{3}}{2}$sin2ωx+$\frac{1}{2}$cos2ωx+$\frac{1}{2}$=sin(2ωx+$\frac{π}{6}$)+$\frac{1}{2}$,
∵f(x)的最小正周期为π,ω>0,
∴$\frac{2π}{2ω}$=π,∴ω=1.
即f(x)=sin(2x+$\frac{π}{6}$)+$\frac{1}{2}$,
令-$\frac{π}{2}$+2kπ≤2x+$\frac{π}{6}$≤$\frac{π}{2}$+2kπ,解得:-$\frac{π}{3}$+kπ≤x≤$\frac{π}{6}$+kπ,k∈Z.
∴函数f(x)的单调递增区间是[-$\frac{π}{3}$+kπ,$\frac{π}{6}$+kπ],k∈Z.
(II)f(A)=sin(2A+$\frac{π}{6}$)+$\frac{1}{2}$,
∴当2A+$\frac{π}{6}$=$\frac{π}{2}$+2kπ即A=$\frac{π}{6}$+kπ时,f(A)取得最大值.
∵0<A<π,∴A=$\frac{π}{6}$.
由正弦定理得$\frac{a}{sinA}=\frac{b}{sinB}$,即$\frac{1}{\frac{1}{2}}=\frac{\sqrt{3}}{sinB}$,解得sinB=$\frac{\sqrt{3}}{2}$,
∴B=$\frac{π}{3}$或B=$\frac{2π}{3}$,
当B=$\frac{π}{3}$时,C=$\frac{π}{2}$,△ABC是直角三角形,不符合题意;
∴B=$\frac{2π}{3}$,C=$\frac{π}{6}$.△ABC是等腰三角形,
∴c=a=1.
点评 本题考查了三角恒等变换,正弦函数的图象与性质,解三角形,属于中档题.

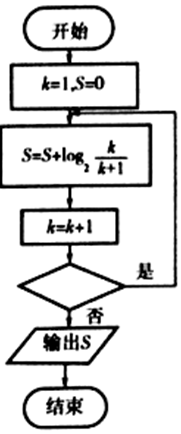
| A. | k<2 | B. | k<3 | C. | k<4 | D. | k<5 |
| A. | $({-∞,-\frac{1}{e}-2e})$ | B. | $({-∞,\frac{1}{e}-e})$ | C. | $({\frac{1}{e}+2e,+∞})$ | D. | $({\frac{1}{e}+e,+∞})$ |
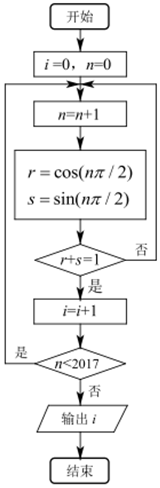 执行如图所示的程序框图,则输出i的值为( )
执行如图所示的程序框图,则输出i的值为( )| A. | 1006 | B. | 1007 | C. | 1008 | D. | 1009 |
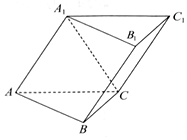 已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.
已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.