题目内容
14.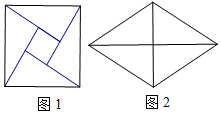 中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )
中国古代数学家赵爽设计的弦图(如图1)是由四个全等的直角三角形拼成,四个全等的直角三角形也可拼成图2所示的菱形,已知弦图中,大正方形的面积为100,小正方形的面积为4,则图2中菱形的一个锐角的正弦值为( )| A. | $\frac{24}{25}$ | B. | $\frac{3}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{7}{25}$ |
分析 由题意,图2是四个全等的直角三角形拼成,只需求出图1中一个直角三角形的小锐角的正余弦值,利用二倍角即可求出图2中菱形的一个锐角的正弦值.
解答 解:由题意,大正方形的面积为100,其边长为10,小正方形的面积为4,其边长为2.
每个直角三角形的面积为$\frac{1}{4}(100-4)=24$.
设图1中一个直角三角形的边长为m,n+2,
可得:$\left\{\begin{array}{l}{\frac{1}{2}m(n+2)=24}\\{{m}^{2}+(n+2)^{2}=1{0}^{2}}\end{array}\right.$,
解得:m=n=6
设小边所对的角为θ,则$sinθ=\frac{6}{10}=\frac{3}{5}$,$cosθ=\frac{4}{5}$,
那么:$sin2θ=2sinθcosθ=\frac{24}{25}$.即图2中菱形的一个锐角的正弦值为$\frac{24}{25}$
故选:A.
点评 本题考查了直角三角形的性质的应用和二倍角公式的计算.属于基础题.

练习册系列答案
相关题目
3.若数列{an}为等差数列,Sn为其前n项和,且a1=2a3-3,则S9=( )
| A. | 25 | B. | 27 | C. | 50 | D. | 54 |
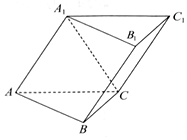 已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.
已知斜三棱柱ABC-A1B1C1中,二面角A1-AC-B是直二面角,∠ABC=90°,BC=2,AC=2$\sqrt{3}$,且AA1⊥A1C,AA1=A1C.
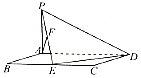 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.
如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.