题目内容
9.函数f(x)是定义在(0,+∞)上的可导函数,f'(x)为其导函数,若x•f'(x)+f(x)=ex(x-1),且f(2)=0,则不等式f(x)<0的解集为( )| A. | (0,1) | B. | (0,2) | C. | (1,2) | D. | (2,+∞) |
分析 构造函数,φ(x)=xf(x),利用导函数的单调性,转化求解不等式的解集即可.
解答 解:函数f(x)是定义在(0,+∞)上的可导函数,f'(x)为其导函数,
令φ(x)=xf(x),则φ′(x)=x•f'(x)+f(x)=ex(x-1),
可知当x∈(0,1)时,φ(x)是单调减函数,并且0•f'(0)+f(0)=e0(0-1)=-1<0,即f(0)<0
x∈(1,+∞)时,函数是单调增函数,f(2)=0,
则φ(2)=2f(2)=0,
则不等式f(x)<0的解集就是xf(x)<0的解集,
不等式的解集为:{x|0<x<2}.
故选:B.
点评 本题考查函数的单调性的应用,不等式的解法,考查转化思想以及计算能力.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
3.若数列{an}为等差数列,Sn为其前n项和,且a1=2a3-3,则S9=( )
| A. | 25 | B. | 27 | C. | 50 | D. | 54 |
14.正四面体ABCD中,M是棱AD的中点,O是点A在底面BCD内的射影,则异面直线BM与AO所成角的余弦值为( )
| A. | $\frac{{\sqrt{2}}}{6}$ | B. | $\frac{{\sqrt{2}}}{3}$ | C. | $\frac{{\sqrt{2}}}{4}$ | D. | $\frac{{\sqrt{2}}}{5}$ |
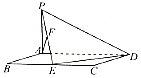 如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.
如图,平行四边形ABCD中,BC=2AB=4,∠ABC=60°,PA⊥AD,E,F分别为BC,PE的中点,AF⊥平面PED.