题目内容
已知a＞0，b＞0，
+
=
，若不等式2a+b≥4m恒成立，则m的最大值为（ ）
| 2 |
| a |
| 1 |
| b |
| 1 |
| 4 |
| A、10 | B、9 | C、8 | D、7 |
考点：基本不等式在最值问题中的应用
专题：计算题,不等式的解法及应用
分析：利用2a+b=4（2a+b）（
+
），结合基本不等式，不等式2a+b≥4m恒成立，即可求出m的最大值．
| 2 |
| a |
| 1 |
| b |
解答：
解：∵a＞0，b＞0，
∴2a+b＞0
∵
+
=
，
∴2a+b=4（2a+b）（
+
）=4（5+
+
）≥36，
∵不等式2a+b≥4m恒成立，
∴36≥4m，
∴m≤9，
∴m的最大值为9，
故选：B．
∴2a+b＞0
∵
| 2 |
| a |
| 1 |
| b |
| 1 |
| 4 |
∴2a+b=4（2a+b）（
| 2 |
| a |
| 1 |
| b |
| 2b |
| a |
| 2a |
| b |
∵不等式2a+b≥4m恒成立，
∴36≥4m，
∴m≤9，
∴m的最大值为9，
故选：B．
点评：本题主要考查了恒成立问题与最值的求解的相互转化，解题的关键是配凑基本不等式成立的条件．
练习册系列答案
挑战100单元检测试卷系列答案
相关题目
函数f（x）=2cos2x-
sin2x（x∈R）的最小正周期和最小值分别为（ ）
| 3 |
| A、2π，3 | B、2π，-1 |
| C、π，3 | D、π，-1 |
定义在[-3，0]∪[2，3]上的函数y=f（x）的图象如图所示，若直线y=a与y=f（x）的图象有两个公共点，则实数a的取值范围为已知数列{an}中，a1=2，an+1=an+
（n∈N+），则a101=（ ）
| 1 |
| 2 |
| A、50 | B、51 | C、52 | D、53 |
设集合U={1，2，3，4，5}，A={2，4}，B={1，2，3}，则图中阴影部分所表示的集合是（ ）
| A、{4} |
| B、{2，4} |
| C、{4，5} |
| D、{1，3，4} |
设全集为R，集合M={x|log2（x-1）＜1}，则∁RM=（ ）
| A、[3，+∞） |
| B、（-∞，1]∪[2，+∞） |
| C、（-∞，1]∪[3，+∞） |
| D、（-∞，0]∪[2，+∞） |
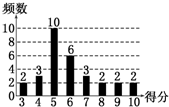为了普及环保知识，增强环保意识，某大学随机抽取30名学生参加环保知识测试，得分（十分制）如图所示，假设得分值的中位数为me，众数为m0，平均值为. |
| x |
A、me=m0=
| ||
B、me=m0＜
| ||
C、me＜m0＜
| ||
D、m0＜me＜
|