题目内容
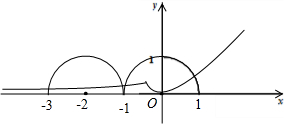
 若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为
若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为考点:函数零点的判定定理
专题:函数的性质及应用
分析:求出函数f(x)=xex的导函数,由导函数等于0求出x的值,以求出的x的值为分界点把原函数的定义域分段,以表格的形式列出导函数在各区间段内的符号及原函数的增减性,从而得到函数的单调区间及极值点,把极值点的坐标代入原函数求极值.然后判断y=|xex|的极值与单调性,然后推出零点的个数.
解答:
解:定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),
∴函数是偶函数,且图象关于x=1对称,
∵函数f(x)=xex的定义域为R,
f′(x)=(xex)′=x′ex+x(ex)′=ex+xex
令f′(x)=ex+xex=ex(1+x)=0,解得:x=-1.
列表:
由表可知函数f(x)=xex的单调递减区间为(-∞,-1),单调递增区间为(-1,+∞).
当x=-1时,函数f(x)=xex的极小值为f(-1)=-
,
y=|xex|,在x=-1时取得极大值:
,x∈(0,+∞)是增函数,
∴x<0时,两个函数图象有3个交点,x>0时,两个函数图象有1个交点.
两个函数图象共有4个交点.
即函数H(x)=|xex|-f(x)在区间[-3,1]上有4个零点.
故答案为:4
∴函数是偶函数,且图象关于x=1对称,
∵函数f(x)=xex的定义域为R,
f′(x)=(xex)′=x′ex+x(ex)′=ex+xex
令f′(x)=ex+xex=ex(1+x)=0,解得:x=-1.
列表:
| x | (-∞,-1) | -1 | (-1,+∞) |
| f′(x) | - | 0 | + |
| f(x) | ↓ | 极小值 | ↑ |
当x=-1时,函数f(x)=xex的极小值为f(-1)=-
| 1 |
| e |

y=|xex|,在x=-1时取得极大值:
| 1 |
| e |
∴x<0时,两个函数图象有3个交点,x>0时,两个函数图象有1个交点.
两个函数图象共有4个交点.
即函数H(x)=|xex|-f(x)在区间[-3,1]上有4个零点.
故答案为:4
点评:本题考查了利用导数研究函数的单调性与极值,在求出导函数等于0的x值后,借助于表格分析能使解题思路更加清晰,此题是中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
△ABC中,M是线段BC的中点且O是线段AM上一个动点,若AM=4,则
•(
+
)的最小值为( )
| OA |
| OB |
| OC |
| A、-4 | B、-12 |
| C、-10 | D、-8 |
已知2a+b=1,a>0,b>0,则
+
的最小值是( )
| 1 |
| a |
| 1 |
| b |
A、2
| ||
B、3-2
| ||
C、3+2
| ||
D、3+
|