题目内容
函数y=x2-x(-1≤x≤1)的值域是 .
考点:函数的值域
专题:计算题,数形结合,函数的性质及应用
分析:先借助于函数y=x2-x在[-1,1]上的图象判断单调性,然后求出函数的值域.
解答:
解:∵函数y=x2-x(-1≤x≤1)的开口向上,对称轴为x=
,顶点为(
,-
),据此做出其图象,
∴函数y=x2-x(-1≤x≤1)在[-1,
]上单调递减,在[
,1]上单调递增,
∴当x=
时,ymin=-
,又∵x=-1时,y=2;x=1时,y=0,∴ymax=2
所以函数y=x2-x(-1≤x≤1)值域为[-
,2].
故答案为[-
,2]
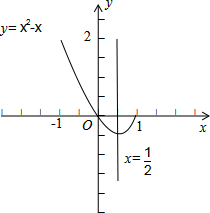
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
∴函数y=x2-x(-1≤x≤1)在[-1,
| 1 |
| 2 |
| 1 |
| 2 |
∴当x=
| 1 |
| 2 |
| 1 |
| 4 |
所以函数y=x2-x(-1≤x≤1)值域为[-
| 1 |
| 4 |
故答案为[-
| 1 |
| 4 |
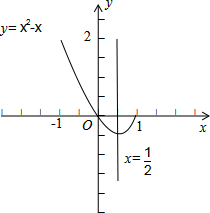
点评:二次函数的值域问题一般是借助于函数图象研究它的单调性,一般先看开口,二看对称轴与区间的关系;有些含有字母的要利用对称轴和区间的关系进行讨论.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点.
如图,在四棱锥P-ABCD中,底面ABCD是平行四边形,且PA⊥底面ABCD,BD⊥PC,E是PA的中点. 若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为
若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为