题目内容
椭圆4x2+9y2=1的长轴长是 ．
考点：椭圆的简单性质
专题：计算题,圆锥曲线的定义、性质与方程
分析：把椭圆的方程化为标准形式，判断焦点所在的坐标轴，求出a的值，即可得到长轴长．
解答：
解：椭圆4x2+9y2=1，即
+
=1，
∴a=
，2a=
，
∴椭圆4x2+9y2=1的长轴长为
，
故答案为：
．
| y2 | ||
|
| x2 | ||
|
∴a=
| 1 |
| 3 |
| 2 |
| 3 |
∴椭圆4x2+9y2=1的长轴长为
| 2 |
| 3 |
故答案为：
| 2 |
| 3 |
点评：本题考查椭圆的标准方程和简单性质，关键是根据标准方程判断焦点的位置并求出长轴长．
练习册系列答案
互动英语系列答案
相关题目
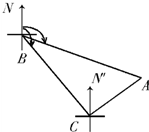如图，货轮在海上以40km/h的速度由B航行到C，航行的方位角∠NBC=140°，A处有灯塔，其方位角∠NBA=110°．在C处观测灯塔A的方位角∠N′CA=35°．由B到C需航行半小时，则C到灯塔A的距离是
若定义在R上的函数f（x）满足f（-x）=f（x），f（2-x）=f（x），且当x∈[0，1]时，其图象是四分之一圆（如图所示），则函数H（x）=|xex|-f（x）在区间[-3，1]上的零点个数为设C={复数}，A={实数}，B={纯虚数}，全集U=C，那么下列结论正确的是（ ）
| A、A∪B=C |
| B、A∩∁UB=∅ |
| C、∁UA=B |
| D、B∪∁UB=C |
在平面内与点A（1，2）距离为1，与点B（4，1）距离为2的直线共有（ ）
| A、1条 | B、2条 | C、3条 | D、4条 |