题目内容
△ABC中,M是线段BC的中点且O是线段AM上一个动点,若AM=4,则
•(
+
)的最小值为( )
| OA |
| OB |
| OC |
| A、-4 | B、-12 |
| C、-10 | D、-8 |
考点:平面向量数量积的运算
专题:平面向量及应用
分析:利用向量的平行四边形法则、数量积运算、基本不等式的性质即可得出.
解答:
 解:如图所示,
解:如图所示,
∵M是线段BC的中点且O是线段AM上一个动点,
∴
+
=2
,
∴
•(
+
)=
•2
=-2|
|•|
|≥-
=-
=-8,当且仅当|
|=|
|=2时取等号.
∴
•(
+
)的最小值为-8.
故选:D.
 解:如图所示,
解:如图所示,∵M是线段BC的中点且O是线段AM上一个动点,
∴
| OB |
| OC |
| OM |
∴
| OA |
| OB |
| OC |
| OA |
| OM |
| OA |
| OM |
(|
| ||||
| 2 |
| 42 |
| 2 |
| OA |
| OM |
∴
| OA |
| OB |
| OC |
故选:D.
点评:本题考查了向量的平行四边形法则、数量积运算、基本不等式的性质,考查了推理能力和计算能力,属于难题.

练习册系列答案
相关题目
设C={复数},A={实数},B={纯虚数},全集U=C,那么下列结论正确的是( )
| A、A∪B=C |
| B、A∩∁UB=∅ |
| C、∁UA=B |
| D、B∪∁UB=C |
在△ABC中,若sinA:sinB:sinC=2:3:4,则cosA的值为( )
A、
| ||
B、
| ||
C、
| ||
D、-
|
有一个山坡,倾斜度为60°,若在斜坡平面上沿着一条与斜坡面和水平面的交线成30°角的直道前进1000米,则实际升高了( )
A、250
| ||
B、250
| ||
C、250
| ||
| D、500米 |
设f(x)、g(x)分别是定义在R上的奇函数和偶函数,g(x)恒不为0,当x<0时,f′(x)g(x)-f(x)g′(x)>0,且f(3)=0,则不等式f(x)g(x)<0的解集是( )
| A、(-3,0)∪(3,+∞) |
| B、(-3,0)∪(0,3) |
| C、(-∞,-3)∪(3,+∞) |
| D、(-∞,-3)∪(0,3) |
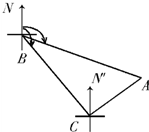 如图,货轮在海上以40km/h的速度由B航行到C,航行的方位角∠NBC=140°,A处有灯塔,其方位角∠NBA=110°.在C处观测灯塔A的方位角∠N′CA=35°.由B到C需航行半小时,则C到灯塔A的距离是
如图,货轮在海上以40km/h的速度由B航行到C,航行的方位角∠NBC=140°,A处有灯塔,其方位角∠NBA=110°.在C处观测灯塔A的方位角∠N′CA=35°.由B到C需航行半小时,则C到灯塔A的距离是 若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为
若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为