题目内容
二项式(ax+
)6的展开式第二项系数为-
,则
x2dx的值为 .
| ||
| 6 |
| 3 |
| ∫ | a -2 |
考点:二项式系数的性质
专题:二项式定理
分析:根据二项式(ax+
)6的展开式第二项系数为-
,求得a的值,从而求得
x2dx的值.
| ||
| 6 |
| 3 |
| ∫ | a -2 |
解答:
解:二项式(ax+
)6的展开式第二项系数为
•a5•
=-
,∴a=-1.
则
x2dx=
x2dx=
x3
=
,
故答案为:
.
| ||
| 6 |
| C | 1 6 |
| ||
| 6 |
| 3 |
则
| ∫ | a -2 |
| ∫ | -1 -2 |
| 1 |
| 3 |
| | | -1 -2 |
| 7 |
| 3 |
故答案为:
| 7 |
| 3 |
点评:本题主要考查求定积分,二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
相关题目
在△ABC中,若sinA:sinB:sinC=2:3:4,则cosA的值为( )
A、
| ||
B、
| ||
C、
| ||
D、-
|
若动点P与定点F(1,1)和直线l:3x+y-4=0的距离相等,则动点p的轨迹是( )
| A、椭圆 | B、双曲线 |
| C、抛物线 | D、直线 |
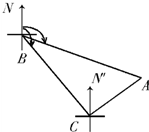 如图,货轮在海上以40km/h的速度由B航行到C,航行的方位角∠NBC=140°,A处有灯塔,其方位角∠NBA=110°.在C处观测灯塔A的方位角∠N′CA=35°.由B到C需航行半小时,则C到灯塔A的距离是
如图,货轮在海上以40km/h的速度由B航行到C,航行的方位角∠NBC=140°,A处有灯塔,其方位角∠NBA=110°.在C处观测灯塔A的方位角∠N′CA=35°.由B到C需航行半小时,则C到灯塔A的距离是 若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为
若定义在R上的函数f(x)满足f(-x)=f(x),f(2-x)=f(x),且当x∈[0,1]时,其图象是四分之一圆(如图所示),则函数H(x)=|xex|-f(x)在区间[-3,1]上的零点个数为