题目内容
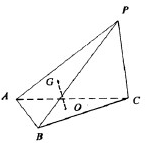 如图,在三棱锥P-ABC中,△ABC是边长等于2的正三角形,且∠PCA=∠PCB.
如图,在三棱锥P-ABC中,△ABC是边长等于2的正三角形,且∠PCA=∠PCB.(Ⅰ)求证:PC⊥AB;
(Ⅱ)设正△ABC的中心为O,△PAB的重心为G,求证:OG∥平面PAC;
(Ⅲ)当侧面PBC⊥底面ABC时,二面角P-AB-C与二面角A-PC-B的大小恰好相等.
①求证:PC⊥底面ABC;
②求二面角A-PB-C的正切值.
考点:与二面角有关的立体几何综合题,直线与平面平行的判定
专题:空间位置关系与距离
分析:(Ⅰ)作AB的中点E,连结PE,CE,有BC=AC,∠PCA=∠PCB,PC=PC,推断出△PBC≌△PAC,进而可知PB=PA,推断出PE⊥AB,又AC=BC,E为AB的中点,推断出CE⊥AB,进而根据线面垂直的判定定理知AB⊥平面PEC,则可证明出PC⊥AB;
(Ⅱ)先根据题意推断出G,O分别在PE,CE上,利用三角形重心的性质推断出
=
,进而推断出OG∥PC,最后根据线面平行的判定定理推断出OG∥平面PAC.
(Ⅲ)①作BC的中点F,连结AF,由AB=AC,推断出AF⊥BC,进而根据面面垂直的性质推断出AF⊥平面BCP,进而可知AF⊥PC,利用线面垂直的判定定理推断出PC⊥平面ABC.
②由PC⊥平面ABC.推断出PC⊥AC,PC⊥BC,判断出∠ACB为二面角A-PC-B,根据PE⊥AB,CE⊥AB,判断出∠PEC为平面APB和平面ABC的二面角,进而可知∠PEC=∠ACB=60°,在Rt△PEC中,求得PC,利用勾股定理求得BP,作FH⊥PB,连结AH,由AE⊥平面BCP,推断出BP⊥AE,进而可知BP⊥平面AFH,根据线面垂直的性质可知BP⊥AH,推断出二面角A-PB-C为∠AHF,根据∠CBP=∠PBC,∠FHB=∠PCB=90°,判断出△BFH∽△BPC,利用
=
,求得FH,最后在Rt△AFH中,求得tan∠AHF.
(Ⅱ)先根据题意推断出G,O分别在PE,CE上,利用三角形重心的性质推断出
| EG |
| GP |
| EO |
| OC |
(Ⅲ)①作BC的中点F,连结AF,由AB=AC,推断出AF⊥BC,进而根据面面垂直的性质推断出AF⊥平面BCP,进而可知AF⊥PC,利用线面垂直的判定定理推断出PC⊥平面ABC.
②由PC⊥平面ABC.推断出PC⊥AC,PC⊥BC,判断出∠ACB为二面角A-PC-B,根据PE⊥AB,CE⊥AB,判断出∠PEC为平面APB和平面ABC的二面角,进而可知∠PEC=∠ACB=60°,在Rt△PEC中,求得PC,利用勾股定理求得BP,作FH⊥PB,连结AH,由AE⊥平面BCP,推断出BP⊥AE,进而可知BP⊥平面AFH,根据线面垂直的性质可知BP⊥AH,推断出二面角A-PB-C为∠AHF,根据∠CBP=∠PBC,∠FHB=∠PCB=90°,判断出△BFH∽△BPC,利用
| BF |
| BP |
| FH |
| PC |
解答:
(Ⅰ)证明:作AB的中点E,连结PE,CE,
∵BC=AC,∠PCA=∠PCB,PC=PC,
∴△PBC≌△PAC,
∴PB=PA,
∴PE⊥AB,
∵AC=BC,E为AB的中点,
∴CE⊥AB,
∵CE?平面PEC,PE?平面PEC,PE∩CE=E,
∴AB⊥平面PEC,
∵PC?平面PEC,
∴PC⊥AB;
(Ⅱ)△PAB的重心为G,△ABC的中心为O,且PE,CE分别为△PAB,△ABC的中线,
∴G,O分别在PE,CE上,
∴
=
=
,
∴OG∥PC,
∵PC?平面APC,OG?平面APC,
∴OG∥平面PAC.
(Ⅲ)①作BC的中点F,连结AF,
∵AB=AC,
∴AF⊥BC,
∵面PBC⊥底面ABC,面PBC∩底面ABC=BC,
∴AF⊥平面BCP,
∵PC?平面BCP,
∴AF⊥PC,
∵PC⊥AB,AB∩AF=A,AB?平面ABC,AF?平面ABC,
∴PC⊥平面ABC.
②∵PC⊥平面ABC.
∴PC⊥AC,PC⊥BC,
∴∠ACB为二面角A-PC-B,
∵PE⊥AB,CE⊥AB,
∴∠PEC为平面APB和平面ABC的二面角,
∴∠PEC=∠ACB=60°,
∴在Rt△PEC中,PC=tan60°•EC=3,
∴BP=
=
,
作FH⊥PB,连结AH,
∵AE⊥平面BCP,
∴BP⊥AE,
∴BP⊥平面AFH,
∵AH?平面AFH,
∴BP⊥AH,
∴二面角A-PB-C为∠AHF,
∵∠CBP=∠PBC,∠FHB=∠PCB=90°,
∴△BFH∽△BPC,
∴
=
,
∴FH=
•PC=
×3=
,
∴在Rt△AFH中,tan∠AHF=
=
=
.

∵BC=AC,∠PCA=∠PCB,PC=PC,
∴△PBC≌△PAC,
∴PB=PA,
∴PE⊥AB,
∵AC=BC,E为AB的中点,
∴CE⊥AB,
∵CE?平面PEC,PE?平面PEC,PE∩CE=E,
∴AB⊥平面PEC,
∵PC?平面PEC,
∴PC⊥AB;
(Ⅱ)△PAB的重心为G,△ABC的中心为O,且PE,CE分别为△PAB,△ABC的中线,
∴G,O分别在PE,CE上,
∴
| EG |
| GP |
| 1 |
| 2 |
| EO |
| OC |
∴OG∥PC,
∵PC?平面APC,OG?平面APC,
∴OG∥平面PAC.
(Ⅲ)①作BC的中点F,连结AF,
∵AB=AC,
∴AF⊥BC,
∵面PBC⊥底面ABC,面PBC∩底面ABC=BC,
∴AF⊥平面BCP,
∵PC?平面BCP,
∴AF⊥PC,
∵PC⊥AB,AB∩AF=A,AB?平面ABC,AF?平面ABC,
∴PC⊥平面ABC.
②∵PC⊥平面ABC.
∴PC⊥AC,PC⊥BC,
∴∠ACB为二面角A-PC-B,
∵PE⊥AB,CE⊥AB,
∴∠PEC为平面APB和平面ABC的二面角,
∴∠PEC=∠ACB=60°,
∴在Rt△PEC中,PC=tan60°•EC=3,
∴BP=
| BC2+PC2 |
| 13 |
作FH⊥PB,连结AH,
∵AE⊥平面BCP,
∴BP⊥AE,
∴BP⊥平面AFH,
∵AH?平面AFH,
∴BP⊥AH,
∴二面角A-PB-C为∠AHF,
∵∠CBP=∠PBC,∠FHB=∠PCB=90°,
∴△BFH∽△BPC,
∴
| BF |
| BP |
| FH |
| PC |
∴FH=
| BF |
| BP |
| 1 | ||
|
3
| ||
| 13 |
∴在Rt△AFH中,tan∠AHF=
| AF |
| FH |
| ||||
|
| ||
| 3 |

点评:本题主要考查了线面平行,线面垂直的判定定理,面面垂直的性质,二面角的计算等.在第三问中,解题的关键是找到所求的二面角的平面.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
函数y=
的定义域为( )
| ||
| lnx |
| A、(0,1)∪(1,+∞) |
| B、(1,+∞) |
| C、(0,1) |
| D、(0,+∞) |
若0<b<a<1,则在ab,ba,aa,bb中最大值是( )
| A、ba |
| B、aa |
| C、ab |
| D、bb |
函数y=x2在区间[1,2]上的平均变化率为( )
| A、4 | B、5 | C、2 | D、3 |
 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2. 如图,四边形ABCD是边长为2的正方形,AE⊥面ABCD,DF∥AE,AE=4,G为EC的中点,且GF∥面ABCD.
如图,四边形ABCD是边长为2的正方形,AE⊥面ABCD,DF∥AE,AE=4,G为EC的中点,且GF∥面ABCD.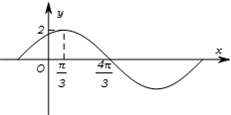 已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<
已知函数f(x)=Asin(ωx+φ)(A>0,ω>0,0<φ<