题目内容
已知函数f(x)=x-
,g(x)=a(2-lnx).若曲线y=f(x)与曲线y=g(x)在x=1处的切线斜率相同,求a的值,并判断两条切线是否为同一条直线.
| 2 |
| x |
考点:利用导数研究曲线上某点切线方程
专题:导数的综合应用
分析:求出两个函数的导函数,得到两函数在x=1时的导数值,由导数值相等求得a的值,然后分别求出两曲线上的
切点,由点斜式求得切线方程,最后加以判断.
切点,由点斜式求得切线方程,最后加以判断.
解答:
解:由f(x)=x-
,g(x)=a(2-lnx),得
f′(x)=1+
,g′(x)=-
.
∴f′(1)=3,g′(1)=-a.
由曲线y=f(x)与曲线y=g(x)在x=1处的切线斜率相同,得
-a=3,即a=-3.
曲线y=f(x)在x=1处的切线方程为y-f(1)=3(x-1),
即y+1=3(x-1),整理得3x-y-4=0.
曲线y=g(x)在x=1处的切线方程为y-g(1)=3(x-1).
即y+6=3(x-1),整理得3x-y-9=0,
∴两条切线不是同一条直线.
| 2 |
| x |
f′(x)=1+
| 2 |
| x2 |
| a |
| x |
∴f′(1)=3,g′(1)=-a.
由曲线y=f(x)与曲线y=g(x)在x=1处的切线斜率相同,得
-a=3,即a=-3.
曲线y=f(x)在x=1处的切线方程为y-f(1)=3(x-1),
即y+1=3(x-1),整理得3x-y-4=0.
曲线y=g(x)在x=1处的切线方程为y-g(1)=3(x-1).
即y+6=3(x-1),整理得3x-y-9=0,
∴两条切线不是同一条直线.
点评:本题考查利用导数研究曲线上某点出的切线方程,过曲线上某点处的切线的斜率,就是函数在该点处的导数值,是中档题.

练习册系列答案
相关题目
△ABC中,A、B满足关系式:
>0,则△ABC是( )
| 1 |
| tanA•tanB |
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、任意三角形 |
已知f(x)=
,则f(
)的值为( )
| sin(π-x)•cos(2π-x) |
| cos(-π-x)•tan(π-x) |
| π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知点A(1,3),B(4,-1),则与向量
方向相反的单位向量为( )
| AB |
A、(
| ||||
B、(-
| ||||
C、(
| ||||
D、(-
|
在线段[0,3]上任取一点,则此点坐标不大于1的概率是( )
A、
| ||
B、
| ||
C、
| ||
D、
|
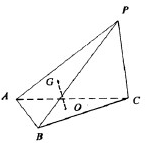 如图,在三棱锥P-ABC中,△ABC是边长等于2的正三角形,且∠PCA=∠PCB.
如图,在三棱锥P-ABC中,△ABC是边长等于2的正三角形,且∠PCA=∠PCB.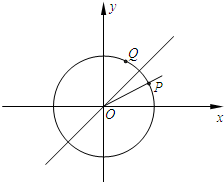 如图,已知单位圆上两点P,Q关于直线y=x对称,且以x轴正半轴为始边、以射线OP为终边的角的大小为x.
如图,已知单位圆上两点P,Q关于直线y=x对称,且以x轴正半轴为始边、以射线OP为终边的角的大小为x.