题目内容
函数y=
的定义域为（ ）
| ||
| lnx |
| A、（0，1）∪（1，+∞） |
| B、（1，+∞） |
| C、（0，1） |
| D、（0，+∞） |
考点：函数的定义域及其求法
专题：函数的性质及应用
分析：根据函数成立的条件，即可求出函数的定义域．
解答：
解：要使函数有意义，则
，
即
，
即x＞0且x≠1，
则函数的定义域为（0，1）∪（1，+∞），
故选：A．
|
即
|
即x＞0且x≠1，
则函数的定义域为（0，1）∪（1，+∞），
故选：A．
点评：本题注意考查函数定义域的求法，要求熟练掌握常见函数成立的条件．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
已知α∈（
，π），且sinα=
，则tan2α=（ ）
| π |
| 2 |
| 3 |
| 5 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
若数列{an}满足：a1=-
，an=1-
（n＞1），则a4=（ ）
| 1 |
| 4 |
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
函数f（x）=2xex在P点处的切线斜率是2，则P点的横坐标为（ ）
| A、2 | B、0 | C、-1 | D、ln2 |
△ABC中，A、B满足关系式：
＞0，则△ABC是（ ）
| 1 |
| tanA•tanB |
| A、锐角三角形 |
| B、钝角三角形 |
| C、直角三角形 |
| D、任意三角形 |
双曲线
-
=-1的焦点的坐标是（ ）
| x2 |
| 4 |
| y2 |
| 9 |
A、（±
| ||
B、（±
| ||
C、（ 0，±
| ||
D、（0，±
|
已知复数z=（cosθ+i）（2sinθ-i）是纯虚数，θ∈[0，2π），则θ=（ ）
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中，已知A=30°，b=2
，a=2，则角B等于（ ）
| 3 |
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
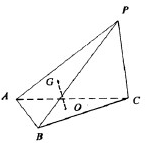如图，在三棱锥P-ABC中，△ABC是边长等于2的正三角形，且∠PCA=∠PCB．