题目内容
若0<b<a<1,则在ab,ba,aa,bb中最大值是( )
| A、ba |
| B、aa |
| C、ab |
| D、bb |
考点:指数函数的图像变换
专题:函数的性质及应用
分析:利用指数函数和幂函数的单调性,可以比较四个数的大小,进而得到在ab,ba,aa,bb的最大值.
解答:
解:∵0<b<a<1,
∴y=ax和y=bx均为减函数,
∴ab>aa,ba<bb,
又∵y=xb在(0,+∞)为增函数,
∴ab>bb,
即在ab,ba,aa,bb中最大值是ab,
故选:C
∴y=ax和y=bx均为减函数,
∴ab>aa,ba<bb,
又∵y=xb在(0,+∞)为增函数,
∴ab>bb,
即在ab,ba,aa,bb中最大值是ab,
故选:C
点评:本题考查的知识点是指数函数的单调性和幂函数的单调性,熟练掌握指数函数的单调性和幂函数的单调性与参数的关系是解答的关键.

练习册系列答案
相关题目
若数列{an}满足:a1=-
,an=1-
(n>1),则a4=( )
| 1 |
| 4 |
| 1 |
| an-1 |
A、
| ||
B、
| ||
C、
| ||
D、-
|
已知复数z=(cosθ+i)(2sinθ-i)是纯虚数,θ∈[0,2π),则θ=( )
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
在△ABC中,已知A=30°,b=2
,a=2,则角B等于( )
| 3 |
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
已知f(x)=
,则f(
)的值为( )
| sin(π-x)•cos(2π-x) |
| cos(-π-x)•tan(π-x) |
| π |
| 6 |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
已知a>b>0,c∈R,则下列不等式恒成立的是( )
| A、ac>bc | ||||
| B、c-a>c-b | ||||
| C、a2<b2 | ||||
D、
|
已知点A(1,3),B(4,-1),则与向量
方向相反的单位向量为( )
| AB |
A、(
| ||||
B、(-
| ||||
C、(
| ||||
D、(-
|
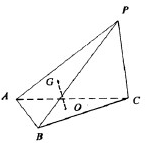 如图,在三棱锥P-ABC中,△ABC是边长等于2的正三角形,且∠PCA=∠PCB.
如图,在三棱锥P-ABC中,△ABC是边长等于2的正三角形,且∠PCA=∠PCB.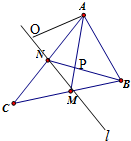 在△ABC中,已知AB=2,AC=6,∠BAC=60°,中线AM、BN交于点P,设
在△ABC中,已知AB=2,AC=6,∠BAC=60°,中线AM、BN交于点P,设