题目内容
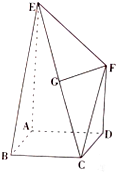如图，四边形ABCD是边长为2的正方形，AE⊥面ABCD，DF∥AE，AE=4，G为EC的中点，且GF∥面ABCD．（Ⅰ）求点B到面EFC的距离；
（Ⅱ）求二面角B-EC-F的余弦值．
考点：用空间向量求平面间的夹角,点、线、面间的距离计算
专题：空间位置关系与距离,空间角,空间向量及应用
分析：由“四边形ABCD是边长为2的正方形，AE⊥面ABCD”可得直线AB、AD、AE两两垂直，因此可以先建立空间直角坐标系，然后将点到平面的距离及二面角的问题转化成空间向量的计算问题解决，主要是平面法向量的应用．
解答：
解析：连AC、BD交于O点，连OG，∵四边形ABCD是正方形，∴O为AC的中点，又∵G为EC的中点，
∴GO∥AE，GO=2，∴GO∥FD，∴G、O、D、F共面，且面GODF∩面ABCD=OD
由GF∥面ABCD得GF∥OD，∴四边形GODF为平行四边形，∴DF=GO=2，
以A为原点，AB、AD、AE所在直线分别为x、y、z轴建立空间直角坐标系如图，
则B（2，0，0），C（2，2，0），E（0，0，4），F（0，2，2）
（1）
=（-2，0，2），
=（0，2，-2），设面EFC的一个法向量为
=（x1，y1，z1），
则
，解得x1=y1=z1，取
=（1，1，1），
则
方向上的单位向量是
=（
，
，
），
=（0，2，0）
∴点B到面EFC之距为d=|
•
|=
．
（2）
=（-2，0，4）
=（0，2，0）
设面BEC的一个法向量为
=（x2，y2，z2），
则
，解得x2=2z2，y=0，取
=（-2，0，-1），
设二面角B-EC-F的大小α，则cosα=
=
=-
．
∴GO∥AE，GO=2，∴GO∥FD，∴G、O、D、F共面，且面GODF∩面ABCD=OD
由GF∥面ABCD得GF∥OD，∴四边形GODF为平行四边形，∴DF=GO=2，
以A为原点，AB、AD、AE所在直线分别为x、y、z轴建立空间直角坐标系如图，
则B（2，0，0），C（2，2，0），E（0，0，4），F（0，2，2）
（1）
| CF |
| EF |
| n1 |
则
|
| n1 |
则
| n1 |
| n0 |
| ||
| 3 |
| ||
| 3 |
| ||
| 3 |
| BC |
∴点B到面EFC之距为d=|
| BC |
| n0 |
2
| ||
| 3 |
（2）
| BE |
| BC |
设面BEC的一个法向量为
| n2 |
则
|
| n2 |
设二面角B-EC-F的大小α，则cosα=
| ||||
|
|
| -3 | ||||
|
| ||
| 5 |
点评：利用空间向量求二面角时，一般是先求出两个平面的法向量
，
，则这两个法向量的夹角或其补角的大小就是所求二面角的大小；利用空间求二面角时，注意结合图形判断二面角是锐角还是钝角．
| n1 |
| n2 |
练习册系列答案
相关题目
在△ABC中，已知A=30°，b=2
，a=2，则角B等于（ ）
| 3 |
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
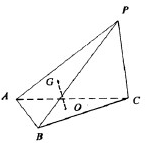如图，在三棱锥P-ABC中，△ABC是边长等于2的正三角形，且∠PCA=∠PCB．
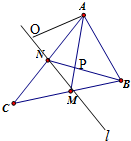在△ABC中，已知AB=2，AC=6，∠BAC=60°，中线AM、BN交于点P，设