题目内容
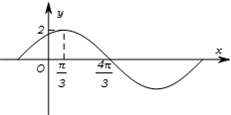已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜| π |
| 2 |
（1）求函数f（x）的解析式；
（2）若f（α+
| π |
| 3 |
| ||
| 5 |
考点：由y=Asin（ωx+φ）的部分图象确定其解析式,两角和与差的正弦函数
专题：三角函数的图像与性质
分析：（1）由函数图象直接得到A和四分之一周期，进一步得到周期，由周期公式求得ω，再由(
，2)在函数图象上代入求解φ的值，则函数解析式可求；
（2）把f（α+
）=
代入（1）中求得的函数解析式，求出cos
的值，由倍角公式求出cosα，结合α的范围进一步求得sinα，则tanα的值可求．
| π |
| 3 |
（2）把f（α+
| π |
| 3 |
| ||
| 5 |
| α |
| 2 |
解答：
解：（1）由图可知：A=2．
∵
=
-
=π，
∴T=4π．
∵ω＞0，
∴ω=
=
=
．
∵图象过点(
，2)，
则2=2sin(
×
+φ)，
即sin(
+φ)=1．
∵0＜φ＜
，
∴φ=
．
故f(x)=2sin(
x+
)；
（2）由f(α+
)=
，得2sin[
(α+
)+
]=
，
∴sin(
α+
)=
，
∴cos
=
，
∴cosα=2cos2
-1=-
，
∵α∈（0，π），
∴sinα=
=
，
∴tanα=
=-
．
∵
| T |
| 4 |
| 4π |
| 3 |
| π |
| 3 |
∴T=4π．
∵ω＞0，
∴ω=
| 2π |
| T |
| 2π |
| 4π |
| 1 |
| 2 |
∵图象过点(
| π |
| 3 |
则2=2sin(
| 1 |
| 2 |
| π |
| 3 |
即sin(
| π |
| 6 |
∵0＜φ＜
| π |
| 2 |
∴φ=
| π |
| 3 |
故f(x)=2sin(
| 1 |
| 2 |
| π |
| 3 |
（2）由f(α+
| π |
| 3 |
| ||
| 5 |
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
| ||
| 5 |
∴sin(
| 1 |
| 2 |
| π |
| 2 |
| ||
| 10 |
∴cos
| α |
| 2 |
| ||
| 10 |
∴cosα=2cos2
| α |
| 2 |
| 4 |
| 5 |
∵α∈（0，π），
∴sinα=
| 1-cos2α |
| 3 |
| 5 |
∴tanα=
| sinα |
| cosα |
| 3 |
| 4 |
点评：本题考查利用y=Asin（ωx+φ）的部分图象求函数解析式，考查了三角函数值得求法，是中档题．
练习册系列答案
相关题目
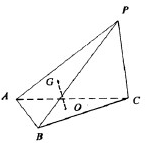如图，在三棱锥P-ABC中，△ABC是边长等于2的正三角形，且∠PCA=∠PCB．
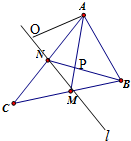在△ABC中，已知AB=2，AC=6，∠BAC=60°，中线AM、BN交于点P，设
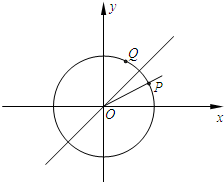如图，已知单位圆上两点P，Q关于直线y=x对称，且以x轴正半轴为始边、以射线OP为终边的角的大小为x．