题目内容
函数y=x2在区间[1，2]上的平均变化率为（ ）
| A、4 | B、5 | C、2 | D、3 |
考点：变化的快慢与变化率
专题：导数的概念及应用
分析：利用函数的解析式求出区间两个端点的函数值，再利用平均变化率公式求出该函数在区间[1，2]上的平均变化率．
解答：
解：∵f（x）=x2，∴f（1）=1，f（2）=4
∴该函数在区间[1，2]上的平均变化率为
=3
故选：D．
∴该函数在区间[1，2]上的平均变化率为
| 4-1 |
| 2-1 |
故选：D．
点评：本题考查函数在区间上的平均变化率，考查学生的计算能力，属于基础题．
练习册系列答案
名校课堂系列答案
相关题目
函数f（x）=2xex在P点处的切线斜率是2，则P点的横坐标为（ ）
| A、2 | B、0 | C、-1 | D、ln2 |
在△ABC中，已知A=30°，b=2
，a=2，则角B等于（ ）
| 3 |
| A、30° |
| B、60° |
| C、30°或150° |
| D、60°或120° |
已知a＞b＞0，c∈R，则下列不等式恒成立的是（ ）
| A、ac＞bc | ||||
| B、c-a＞c-b | ||||
| C、a2＜b2 | ||||
D、
|
已知点A（1，3），B（4，-1），则与向量
方向相反的单位向量为（ ）
| AB |
A、（
| ||||
B、（-
| ||||
C、（
| ||||
D、（-
|
如图，在四棱锥P-ABCD中，底面ABCD是菱形，PA=PB，且侧面PAB⊥平面ABCD，点E是棱AB的中点．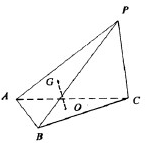
如图，在三棱锥P-ABC中，△ABC是边长等于2的正三角形，且∠PCA=∠PCB．