题目内容
计算:
2xexdx= .
| ∫ |
考点:定积分
专题:导数的综合应用
分析:由分部积分法可得
2xexdx=2xex-ln2
ex2xdx,解方程可得.
| ∫ |
| ∫ |
解答:
解:由分部积分法可得
2xexdx=
2xdex=2xex-
exd2x
=2xex-
ex2xln2dx=2xex-ln2
ex2xdx,
∴(1+ln2)
ex2xdx=2xex,
∴
2xexdx=
2xex
故答案为:
2xex
| ∫ |
| ∫ |
| ∫ |
=2xex-
| ∫ |
| ∫ |
∴(1+ln2)
| ∫ |
∴
| ∫ |
| 1 |
| 1+ln2 |
故答案为:
| 1 |
| 1+ln2 |
点评:本题考查分部积分法求解不定积分,属基础题.

练习册系列答案
相关题目
已知空间中的直线l和两个不同的平面α、β,且l?α,l?β.若α⊥β,则命题p:“l⊥β”是命题q:“l∥α”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
设p:x∈{x|y=lg(x-1)},q:x∈{x|2-x<1},则p是q的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
已知i是虚数单位,若z(1+3i)=i,则z的虚部为( )
A、
| ||
B、-
| ||
C、
| ||
D、-
|
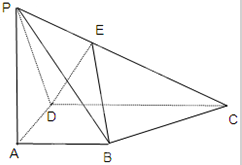 如图,PA⊥平面ABCD,底面ABCD是直角梯形,AB⊥AD,AB=AD,CD=2AB,E为PC中点.若PB与平面ABCD所成的角为45°
如图,PA⊥平面ABCD,底面ABCD是直角梯形,AB⊥AD,AB=AD,CD=2AB,E为PC中点.若PB与平面ABCD所成的角为45° 在直三棱住ABC-A1B1C1,中CA=CB=CC1=2,∠ACB=90°.E、F分别是BC、A1A的中点.
在直三棱住ABC-A1B1C1,中CA=CB=CC1=2,∠ACB=90°.E、F分别是BC、A1A的中点.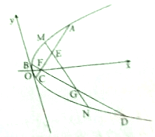 如图,已知抛物线C:y2=2px(p>0)的焦点F(1,0)过点F作任何两条弦AC,BD,且
如图,已知抛物线C:y2=2px(p>0)的焦点F(1,0)过点F作任何两条弦AC,BD,且