题目内容
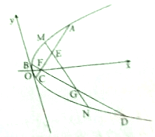 如图,已知抛物线C:y2=2px(p>0)的焦点F(1,0)过点F作任何两条弦AC,BD,且
如图,已知抛物线C:y2=2px(p>0)的焦点F(1,0)过点F作任何两条弦AC,BD,且| AC |
| BD |
(1)写出抛物线C的方程;
(2)直线EG是否过定点?若过,求出该定点,若不过,说明理由;
(3)设直线EG交抛物线C于M,N两点,试求|MN|的最小值.
考点:抛物线的简单性质
专题:综合题,圆锥曲线的定义、性质与方程
分析:(1)由已知得
=1,由此能求出抛物线C的方程.
(2)直线EG过定点(3,0),设A(x1,y1),C(x2,y2),直线AC的方程为x=my+1,代入抛物线C1的方程,得y2-4my-4=0,由此能求出直线过定点H(3,0);
(3)直线EG的方程为x=ty+3,代入抛物线方程,利用两点间的距离公式,即可求得结论
| p |
| 2 |
(2)直线EG过定点(3,0),设A(x1,y1),C(x2,y2),直线AC的方程为x=my+1,代入抛物线C1的方程,得y2-4my-4=0,由此能求出直线过定点H(3,0);
(3)直线EG的方程为x=ty+3,代入抛物线方程,利用两点间的距离公式,即可求得结论
解答:
解:(1)∵抛物线C:y2=2px(p>0)的焦点F(1,0),
∴
=1,解得p=2,
∴抛物线C的方程为y2=4x.
(2)直线EG过定点(3,0),
设A(x1,y1),C(x2,y2),直线AC的方程为x=my+1,
代入抛物线C的方程,得y2-4my-4=0,由此能求出直线过定点H(3,0);
则y1+y2=4m,x1x2=4m2+2,
∴AC的中点坐标为E(2m2+1,2m),
由AC⊥BD,得BD的中点坐标为G(
+1,-
),
令2m2+1=
+1,得m2=1,此时2m2+1=
+1=3,
故直线过点H(3,0),
当m2≠1时,kHE=
,
同理kHG=
,
∴kHE=kHG,
∴E,H,G三点共线,
故直线过定点H(3,0);
(3)设M(
,yM),N(
,yN),直线EG的方程为x=ty+3,代入抛物线方程可得y2-4ty-12=0,
∴yM+yN=4t,yMyN=-12,
∴|MN|2=(
-
)2+(yM-yN)2=16(t2+3)(t2+1)≥48,
∴|MN|≥4
,
当t=0,即直线EG垂直于x轴时,|MN|取得最小值4
.
∴
| p |
| 2 |
∴抛物线C的方程为y2=4x.
(2)直线EG过定点(3,0),
设A(x1,y1),C(x2,y2),直线AC的方程为x=my+1,
代入抛物线C的方程,得y2-4my-4=0,由此能求出直线过定点H(3,0);
则y1+y2=4m,x1x2=4m2+2,
∴AC的中点坐标为E(2m2+1,2m),
由AC⊥BD,得BD的中点坐标为G(
| 2 |
| m2 |
| 2 |
| m |
令2m2+1=
| 2 |
| m2 |
| 2 |
| m2 |
故直线过点H(3,0),
当m2≠1时,kHE=
| m |
| m2-1 |
同理kHG=
| m |
| m2-1 |
∴kHE=kHG,
∴E,H,G三点共线,
故直线过定点H(3,0);
(3)设M(
| yM2 |
| 4 |
| yN2 |
| 4 |
∴yM+yN=4t,yMyN=-12,
∴|MN|2=(
| yM2 |
| 4 |
| yN2 |
| 4 |
∴|MN|≥4
| 3 |
当t=0,即直线EG垂直于x轴时,|MN|取得最小值4
| 3 |
点评:本题考查抛物线方程的求法,考查弦长的最小值的求法,考查直线是否过定点坐标的判断与求法,考查直线与抛物线的位置关系.解题时要认真审题,注意韦达定理和弦长公式的合理运用.

练习册系列答案
相关题目