题目内容
计算抛物线y=x2-3x+2上任一点P(μ,v)处的切线的斜率,并求出抛物线顶点处切线的方程.
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用,直线与圆
分析:求出函数的导数,求得切点处的切线的斜率,求出函数的顶点和切线的斜率,即可得到顶点处的切线方程.
解答:
解:y=x2-3x+2的导数为y′=2x-3,
即有任一点P(μ,v)处的切线的斜率为2μ-3.
在抛物线顶点(
,-
)处切线的斜率为k=2×
-3=0,
即有抛物线顶点处切线的方程为y=-
.
即有任一点P(μ,v)处的切线的斜率为2μ-3.
在抛物线顶点(
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 2 |
即有抛物线顶点处切线的方程为y=-
| 1 |
| 4 |
点评:本题考查导数的运用:求切线方程,掌握导数的几何意义,是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
复数z=1+
的虚部为( )
| 1 |
| i |
| A、1 | B、i | C、-1 | D、-i |
如图所示,AC1是正方体的一条体对角线,点P,Q分别为其在棱的中点,则PQ与AC1所成的角为( ) 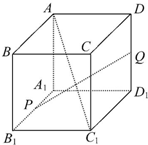

A、
| ||
B、
| ||
C、
| ||
D、
|